How much can we trust life tables? Sensitivity of mortality measures to right-censoring treatment

Abstract

International organizations, research institutions, insurance companies, pension funds and health policymakers calculate human mortality measures from life tables. Life-table data, though, are usually right-censored; that is, the last open-end age group does not contain information about the exact ages at death of individuals there, and mortality measures are sensitive to the way censoring is addressed. The standard way of “closing” the life table assumes a constant hazard of death for the last age group. This might lead to erroneous conclusions about mortality measures, especially when the open-end age interval contains a large proportion of the study population. In this article, we propose, instead, fitting a parametric model that well describes human mortality patterns, the gamma-Gompertz-Makeham, accounting for censoring, and constructing model-based equivalents of five mortality measures: life expectancy, the modal age at death, life disparity, entropy and the Gini coefficient. We show that, in comparison to conventional life-table measures, model-based measures are less sensitive to the age at censoring or, equivalently, to the proportion of censored individuals, and can be only slightly distorted even if the age at censoring is low. This study also compares life-table and model-based mortality measures for a non-human population with an underlying Gompertz mortality schedule in which a fixed proportion of the population is censored. Using model-based mortality measures is essential when studying the mortality of populations subjected to substantial censoring; for instance, many life tables for developing countries contain an open-end interval that contains more than 10% of the population. In this study, we show that life expectancy at birth for Brazilian females in 2007, calculated by standard life-table algebra, exceeds by almost 3 years the gamma-Gompertz-Makeham model-based life expectancy. This article might serve as a basis for recalculation of mortality measures for all populations subjected to substantial censoring.

Right-censoring and life-table mortality measures

Human mortality data are aggregated in life tables that describe the distribution of deaths in a given period (or cohort) and directly provide mortality measures such as the age-specific death rates and (remaining) life expectancy at each age. Statistical offices, international organizations, research institutions, insurance companies, pension funds and health policymakers calculate, compare and project a number of mortality and longevity measures derived from the life table. However, statistical offices often provide age-specific death counts up to a given age x_C (for example, x_C=80, 85, 90, 95, 100) aggregating all subsequent death counts in a “x_C+” group, that is, mortality data are right-censored.

Life expectancy, perhaps the most widely used longevity measure, is sensitive to the way we address right-censoring, that is, what we assume about the exposure in the last (open-end) age group. The _na_x column of the life table contains the average number of person-years lived between ages x and x+n by an individual who died in this interval. In the absence of accurate individual data, _na_x are usually taken either from the Coale and Demeny (1966) model life tables or by assuming n/2 exposure in all intervals [x, x+n), but the first (capturing infant mortality) and the last (open-age) one (Wilmoth et al., 2007). Remaining life expectancy at any age x, calculated by life-table algebra, depends on the choice of the _na_x column and especially on _∞a_x, the average number of person-years lived by an individual that dies in the last open-age interval. The standard assumption is that _∞a_x equals the reciprocal of the death rate in the last age category: _∞a_x=1/m_x, that is, after the last available age in the life-table individuals are exposed to a constant hazard¹ of death (Preston et al., 2001). This is a strong assumption that might not be empirically justified, especially when the open-end interval starts at an age with a high mortality rate: modifying _∞a_x leads to a completely new age vector of _nL_x that affects remaining life expectancies at all ages.

Life tables impose a mortality model on the last open-end age group. When this model does not reflect the preceding age pattern of mortality, the associated mortality measures will be distorted: the bigger the proportion of observations subjected to this type of censoring, the larger the distortion. Life tables for many (historical and contemporary) populations leave 10% or more of the population in the open-end interval (see Table 2), which questions the resulting mortality indicators, such as life expectancy, life disparity, entropy, or the Gini coefficient, that are widely used by governments, international organizations and insurance companies. The credibility of reported mortality measures for many developing countries is questionable because the open-end age group contains a substantial proportion of the population. This problem is to be observed not only in historical populations, for example Bangladeshi life tables from 1974 to 1981 that end up with a 65+ or a 70+ open-end interval containing between 26% and 55% of the population (HLD, 2015), but also in contemporary life tables like the ones for Brazil in 2007—the last 80+ age group contains 34.16% of males and 50.89% of females.²

In this article, we address right censoring in a typical survival-analysis setting. We fit a parametric model, the gamma-Gompertz-Makeham (ΓGM, throughout the paper) assuming that the death counts D(x) at adult ages x are Poisson-distributed (Brillinger, 1986), that is, D(x)~Poisson (E(x)μ(x)), where E(x) denotes age-specific exposure and μ(x) is the ΓGM hazard of death at age x:

$$\begin{array}{}\text{(1)}& \mu (x)=\frac{a{e}^{bx}}{1+\frac{a\gamma }{b}(e^{bx}-\mathrm{1)}}+c.\end{array}$$

Parameter a denotes the level of senescent mortality at the starting age of analysis, b is the rate of individual aging, c is an age-constant external risk of death that is, in general, not related to the aging process, and γ equals the squared coefficient of variation of the distribution of unobserved heterogeneity (frailty). The ΓGM frailty model is widely used in human mortality research as it captures well the S-shaped pattern of mortality at adult ages. For detailed discussion on the semantics and mathematics behind the ΓGM we redirect our readers to Vaupel et al. (1979), Missov and Finkelstein (2011), Vaupel and Missov (2014) and Missov and Vaupel (2015). We use maximum likelihood for fitting the ΓGM model, that is, we maximize a Poisson log-likelihood

$$\begin{array}{}\text{(2)}& \ln L=\sum _x[D(x)\ln \mu (x)-E(x)\mu (x)],\end{array}$$

in which E(x) contains all the information on censoring.

We compute model-based equivalents of five frequently used mortality measures (remaining life expectancy, the modal age at death, life disparity, entropy and the Gini coefficient) that are based on the estimated ΓGM parameters. We illustrate the lower sensitivity of model-based mortality measures to the age at censoring in comparison to their life-table counterparts. As model-based mortality measures are only slightly distorted even when the age at censoring is low (or, what is equivalent, the proportion of censored individuals is high), we argue that international organizations, research institutions, insurance companies, pension funds and even evolutionary biologists working with non-human life tables should use model-based mortality measures.

ΓGM model-based mortality measures

We will focus on the five perhaps most widely used mortality measures: e(x), remaining life expectancy at age x; M, the modal age at death; e^†, life disparity; H, entropy; and G, the Gini coefficient. For life-table calculation of these (and other) mortality measures we refer the reader to Shkolnikov and Andreev (2010), the only exception being the modal age at death. To avoid random fluctuation in the density of deaths that might affect M (see Fig. 1), we apply LOESS smoothing (“loess” function in the “stats” R-package) with a smoothing parameter equal to 0.25. The modal age at death is taken then with high precision directly from the values interpolated by LOESS.

• 1 Remaining life expectancy at x (x⩾0) provides the average remaining lifespan of survivors to age x. It is calculated as

  $$\begin{array}{}\text{(3)}& e(x)=\frac{1}{s(x)}{\int }_x^{\infty }s(t)dt,\end{array}$$

  where s(x) denotes the survival function of the distribution of deaths. A ΓGM life expectancy can be calculated by either substituting the ΓGM survival function

  $$\begin{array}{}\text{(4)}& s(x)=e^{-cx}{\left(1+\frac{a\gamma }{b}(e^{bx}-\mathrm{1)}\right)}^{-\frac{1}{\gamma }},\end{array}$$

  in (3) and taking the resulting integral numerically or taking advantage of a closed-form expression containing hypergeometric series (see Missov and Lenart, 2013, Section 2.3: 30–31).

• 2 The modal age at death M, that is the age of highest concentration of deaths in a population, is an important indicator for policymakers as this is the age around which public health spends most of its resources. The modal age at death in a ΓGM is determined by maximizing μ(x) · s(x) (see equations (1) and (4)).

• 3 Life disparity e^† measures, on the one hand, how much lifespans differ among individuals and, on the other hand, how many life years are lost because of death (Keyfitz, 1977). It is defined as the average remaining life expectancy at ages when deaths occur:

  $$\begin{array}{}\text{(5)}& e^{†}={\int }_0^{\infty }e(x)\mu (x)s(x)dx=-{\int }_0^{\infty }s(x)\ln s(x)dx.\end{array}$$

  In a ΓGM setting, e^† is calculated by numerical integration of (5) taking s(x) from (4).

• 4 Entropy H measures heterogeneity in the age at death or, alternatively, the elasticity of life expectancy with respect to proportional changes in age-specific mortality (Keyfitz, 1977). It is defined as

  $$\begin{array}{}\text{(6)}& H=\frac{-{\int }_0^{\infty }s(x)\ln s(x)dx}{{\int }_0^{\infty }s(x)dx}=\frac{e^{†}}{e\mathrm{(0)}}.\end{array}$$

  In a ΓGM setting, we take s(x) from (4) and calculate e(0) and e^† from (3) and (5), respectively.

• 5 For a given population, the Gini coefficient G measures inter-individual inequality in the length of life (Shkolnikov et al., 2003). It is defined as

  $$\begin{array}{}\text{(7)}& G\mathrm{=1}-\frac{{\int }_0^{\infty }{s}^2(x)dx}{{\int }_0^{\infty }s(x)dx}\mathrm{=1}-\frac{{\int }_0^{\infty }{s}^2(x)dx}{e\mathrm{(0)}}.\end{array}$$

  G can be also represented as the mean of the absolute differences in individual ages of death relative to life expectancy (Kendall and Stuart, 1966). The range of the Gini coefficient is [0, 1] with 1 representing a population in which all deaths occur at the same time. In most developed countries, the Gini coefficient increases with time as many early deaths are postponed to later ages. Demographers address this phenomenon as “life-table rectangulatization” referring to the shape of the corresponding survival curve (Shkolnikov et al., 2003). In a ΓGM setting, we calculate the Gini coefficient by substituting (4) in (7) and integrating the corresponding expressions numerically.

Figure 1

The effect of random fluctuation on the identification of the modal age at death (identified by a dashed line). The red curve corresponds to the d_x column for the Swedish male population in 1970 (Source: HMD, 2015). Without smoothing, the modal age at death is misspecified by about 3 years because of random fluctuation. The ΓGM fit (blue curve) is almost identical to the non-parametrically smoothed (by LOESS) d_x (green curve).

Life-table vs model-based mortality measures

Life-table mortality measures depend on the way the life table is “closed”, that is, on the assumption about exposure in the last (open-age) interval. Most often life-table calculations are based on the assumption that the hazard after the age at censoring x_C is constant (Preston et al., 2001), and the lower x_C, the more unrealistic this assumption (the force of mortality at adult ages has an S-shaped strictly increasing pattern). In this section, we illustrate by how much life-table mortality measures can be distorted if the age at censoring is low, that is, when a high proportion of individuals is censored. While the latter is rather rarely seen in human mortality data, perhaps except for some developing countries, it is common practice in experiments with non-human species—researchers wait until a certain (not necessarily high) percentage of the organisms die. We show for both human and non-human data that model-based mortality measures must be used because they accurately account for censoring. As a result they can only be slightly distorted even if the age at censoring is low, that is, when the proportion of censored individuals is high. To illustrate that this effect is not restricted to the ΓGM model, that is, to the model that describes best adult human mortality (Missov and Vaupel, 2015), we consider an additional example with experimental non-human data (rats), where the mortality pattern is well captured by a Gompertz model.

Sensitivity to censoring in human mortality

We simulate individual lifespans from a ΓGM model: the generating parameters correspond to the estimated ΓGM parameters (a=3.28 · 10⁻⁴, b=0.105, c=6.52 · 10⁻⁴ and γ=0.094) for Swedish males in 1970, ages 25–110. Our choice fell on this population because of its clear S-shaped mortality pattern. We aggregate the death counts and exposures age-wise to construct a life table. We compare then five life-table mortality measures—remaining life expectancy, the modal age at death, life disparity, entropy and the Gini coefficient—to their ΓGM model-based counterparts, knowing the true value of each measure.

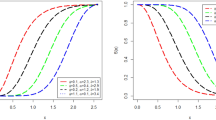
Figures 2 and 3 show the life-table vs model-based versions of the five mortality measures (we considered remaining life expectancy at two ages: 25 and 50) for populations of size 10,000 and 200,000, respectively. If the age at censoring is not lower than 85, life-table measures deviate slightly from their true values (see Table 1). It is not surprising that discrepancy increases as the age at censoring x_C gets lower. However, even for x_C between 75 and 85, all five life-table measures are already distorted by 10–20%. While the statistical offices in many countries “close” their life tables at least at age 85, there is a number of countries in which the last open-age group starts at lower ages (Wilmoth et al., 2007). As a result, their mortality indicators can potentially be distorted if calculated by conventional life-table algebra. Note that the proportion of censored individuals is much more important than the age at censoring. In the simulation example an 85+ open-end interval corresponds to about 20% censoring, while the 85+ age group in the Brazilian life tables for 2007 contains 34.16% of male and 50.89% of female deaths (HLD, 2015).

Figure 2

Life-table (red) versus ΓGM model-based (blue) mortality measures for a population of size 10,000. Individual lifetimes have been simulated from a ΓGM (1,000 repetitions): the resulting death counts and exposures have been aggregated age-wise. The red dashed line in each graph denotes the true value of the measure.

Figure 3

Life-table (red) versus ΓGM model-based (blue) mortality measures for a population of size 200,000. Individual lifetimes have been simulated from a ΓGM (1,000 repetitions): the resulting death counts and exposures have been aggregated age-wise. The red dashed line in each graph denotes the true value of the measure.

Table 1 Difference between median and true life-table mortality measures for different ages at censoring (simulation example from Fig. 3). Percentage of over- or underestimation are given in parentheses

Sensitivity to censoring in non-human mortality

Experimental mortality data for non-human species are often characterized by heavy censoring, leaving sometimes only a small proportion of fully observed individuals. Human mortality data are typically subjected to type-I censoring (with a fixed age at censoring), while experimental data often exhibit random or deterministic censoring. Depending on the experimental setup, we can observe type-I, type-II (experiment ends when a fixed proportion of the organisms die, for example, Dawidowicz et al., 2010; Pietrzak et al., 2015), or, more rarely, hybrid censoring (experiment ends when a fixed proportion of the organisms die or a given age is reached, see Balakrishnan and Kundu, 2013). Here we focus on the effect of type-II censoring on the mortality measures for a population of rats (Anisimov et al., 1989). The mortality pattern in this dataset, unlike the human one, is not captured by the ΓGM model: Lenart and Missov (2014) apply a goodness-of-fit test for the Gompertz distribution to verify the exponential increase in the hazard of death. The hazard of the Gompertz model is given by (1) for c=γ=0. We calculate model-based mortality measures by performing parametric bootstrapping (1,000 repetitions). Note that parameter estimation is carried out by maximizing a Gompertz likelihood as we deal with individual data (for aggregated data, as it is in the case of human mortality, we maximize a Poisson likelihood, see section ‘Right-censoring and life-table mortality measures’ and equation (2)).

Figure 4 illustrates the distortions in rat mortality measures when type-II censoring is addressed in a life-table style. Depending on the proportion of censored individuals (from 0 to 70%), life expectancy and the modal age at death can be mismatched on average by up to 100 days, life disparity and entropy can be calculated as much as twice as low, while the Gini coefficient can be off by 10%.

Figure 4

Life-table (red) versus ΓGM model-based (blue) mortality measures for a rat population of size 200 (1,000 repetitions, simulation based on the estimates by Lenart and Missov (2014) for the dataset in Anisimov et al. (1989)). The red dashed line in each graph denotes the true value of the measure.

Discussion

Mortality measures calculated from conventional life tables, that is, constructed on the basis of raw death counts, might be misleading because of the way right censoring is addressed: in the last open-end age group, life tables assume a constant hazard equal to the death rate in the beginning of the interval. The latter, constructed as the ratio of raw death counts over exposure, can be higher or lower than the “true” hazard. If it is lower, remaining life expectancy at any preceding age will be overestimated. If, on the contrary, the death rate at the starting age of the last interval exceeds the “true” force of mortality, then remaining life expectancy will be overestimated (underestimated) if area A is smaller (bigger) than area B (see Fig. 5).³

Figure 5

Log-mortality of Swedish males in 1970: raw data (circles), HMD data—raw data until age 95 and Kannisto-smoothed data from age 96 onwards (squares), and ΓGM fit (solid line). The three dashed horizontal lines (corresponding to censoring ages 94, 96 and 100) reflect the assumption that the hazard in the last open-age group in a life table is constant. If the observed death rate at the age at censoring overestimates the true force of mortality, remaining life expectancy will be overestimated/underestimated if the differences between areas A and B is negative/positive. If the observed death rate at the age at censoring underestimates the true force of mortality, remaining life expectancy will be overestimated.

The Human Mortality Database (HMD) (2015) smooths mortality rates at the oldest ages. If statistical offices provide censored (at age x_C) data, age-specific mortality reconstruction from x_C onwards is performed by fitting a Kannisto model to the last 20 ages with available age-specific death counts and extrapolating the estimated model to subsequent ages (Wilmoth et al., 2007). If exact death counts are available for every single age, the HMD smooths the death counts after the first age x_T, at which the number of deaths is lower than 100, by fitting a Kannisto model from age x_T to age 110 (Wilmoth et al., 2007). The hazard of death at age x in a Kannisto model is given by

$$\begin{array}{}\text{(8)}& {\mu }_K(x)=\frac{a{e}^{b(x-x_0)}}{1+a{e}^{b(x-x_0)}},\end{array}$$

where x₀ is the starting age of analysis, while ln a and b represent the intercept and the slope, respectively, of the (assumed) logit(μ_K(x)) linear increase. The Kannisto hazard has an S-shaped (logistic) pattern. Fitting a Kannisto or a gamma-Gompertz-Makeham model to adult human mortality (until age 110) is equivalent as the two models differ only asymptotically—μ_K(x) tends to 1, while the ΓGM allows more flexibility about the plateau: $\mu (x)\underset{x\to \infty }{⟶}b/\gamma +c$. Human mortality measures calculated from the Kannisto-adjusted HMD life tables are almost identical to the ΓGM measures even if the two models are fitted over different age ranges (as in Fig. 5). On the other hand, mortality measures calculated from life tables based on raw mortality data, for example, for countries that are not present in the HMD and rely on standard life-table methodology without applying any mortality model, can be substantially distorted. This can also be the case for human mortality data by cause of death, for hunter-gatherer populations or non-human species, where the proportion of censored individuals can be high.

Mortality measures for countries with lower data quality

The Human Life-Table Database (HLD, 2015) contains life tables for countries with lower mortality-data quality (for detailed selection criteria to HMD and HLD see Shkolnikov et al., 2007; Wilmoth et al., 2007). Reported official mortality measures for HLD countries are based on these datasets. However, apart from other problems HLD data may contain (Shkolnikov et al., 2007), the last age group in many life tables, for historical and contemporary populations, contains a substantial proportion of the population (see Table 2). This questions the adequacy of life-table algebra to calculate mortality measures for these countries.

Table 2 A list of HLD countries whose last available life table (after 1990) has at least 10% censored individuals for at least one of the genders

There are alternative ways of “closing” the life table, apart from the one described in Preston et al., 2001. For example, the constant hazard in the last age group can be adjusted for the growth rate of this group (see Horiuchi and Coale, 1982: equation (7), p. 322). The resulting rate is addressed by Horiuchi and Coale (1982) as the “death rate for the open interval” (DROI). Another option (used in HLD) is to calculate life expectancy at the censoring age ω by a “table of correspondence between e_ω and e₀” (Shkolnikov et al., 2007)⁴ and then adjust the (constant) death rate in the open-end interval. No matter how the constant hazard in the last age group is determined, aggregate mortality measures will be distorted, unless the level of mortality is chosen in such a way that area A equals area B (Fig. 5). Another alternative (that does not assume constant mortality) is to redistribute the deaths in the open-end interval uniformly up to a fixed maximal age. In this case, mortality measures are stable with respect to the choice of the age at censoring, but their accuracy is not satisfactory, especially when the chosen maximal age increases. In the following section we study Brazilian mortality data from 2007 and demonstrate that all these methods for “closing” the life table can lead to erroneous conclusions about the magnitude of life expectancy.

Example: 2007 gender-specific life tables for Brazil

Contemporary Brazilian life tables are characterized by a large proportion of censored individuals. The 80+ open-end age group in 2007 contains over one third (34.16%) of male and over one half (50.89%) of female deaths. To estimate a ΓGM model, age-specific population (or death) counts must be available.⁵ However, such data are missing for a number of HLD populations, which restricts the application of ΓGM-smoothing to the corresponding life tables.

Tables 3 and 4 present remaining life expectancy at age 25 for Brazilian females and males in 2007, assuming for the last age interval (1) a constant hazard (according to Preston et al. (2001),Shkolnikov et al. (2007) used for some populations from HLD, and Horiuchi and Coale (1982), 2) a uniform distribution of deaths with maximal ages 100, 115 and 120, or (3) a ΓGM model. The Brazilian Institute of Geography and Statistics (IBGE) follows Preston et al. (2001) to “close” its life tables, while for some populations HLD uses the “tables of correspondence” that link life expectancy at different ages based on historical progression of mortality in Sweden and France (Shkolnikov et al., 2007). When the age at censoring decreases (and the respective share of censored observations increases), life expectancy is stable in cases (2) and (3), while according to (1) it becomes unrealistically high. The ΓGM e₂₅ increases by about 3 years when more than 2/3 of the population is censored, and e₂₅ for uniformly distributed deaths in the last interval tends to be most realistic if the maximal age is 100. This is to be observed for life expectancy at birth, too (Tables 5 and 6). Note that life expectancy at birth reported by IBGE exceeds the ΓGM one by almost 3 years for females (76.44 versus 73.71) as around half of the deaths are censored, while for males, where about 1/3 of the individuals are censored, the two values are very close (68.82 versus 68.45).

Table 3 Remaining life expectancy at age 25 for Brazilian females in 2007 calculated by assuming a constant hazard in the last age group

Table 4 Remaining life expectancy at age 25 for Brazilian males in 2007 calculated by assuming a constant hazard in the last age group

Table 5 Life expectancy at birth for Brazilian females in 2007 calculated by assuming a constant hazard in the last age group

Table 6 Life expectancy at birth for Brazilian males in 2007 calculated by assuming a constant hazard in the last age group

We incorporated the adjustment by Horiuchi and Coale (1982) for four different growth rates of the last age group (0.5%, 1%, 2% and 5%). Tables 3–6 show that the resulting DROI do not remove the bias associated with the constant-hazard assumption in the open-end interval. As a result, it is only the ΓGM that provides coherent remaining life expectancy values no matter how low the censoring age or, what is equivalent, how large the proportion of censored individuals.

Conclusion

The life-table distribution of deaths is characterized by a constant hazard for the last open-end age interval. This is not a typical approach for treating censoring in survival analysis. Instead we propose fitting a parametric model (when a parametric model provides a satisfactory fit) by accounting for the censoring mechanism and using model-based mortality measures instead of their widely used life-table equivalents because the former are less sensitive to the age at censoring. Current life tables for many countries contain a large proportion of censored individuals, and we suggest calculating the corresponding mortality measures, especially life expectancy, by fitting a gamma-Gompertz-Makeham model because it captures well adult mortality, as well as addresses censoring accurately. If fitting a a gamma-Gompertz-Makeham model is not feasible, that is when age-specific death counts are not available, the most robust (with respect to censoring) life-expectancy estimates among the ones presented in Figs. 3–6 are provided by assuming a uniform distribution of deaths in the open-end interval. Their accuracy, though, depends on the choice of the maximal age: for Brazilian data in 2007 the highest accuracy was provided by uniform distribution of deahts from age 85 to age 100, but this cannot necessarily be the case for other populations. Therefore, we suggest fitting a gamma-Gompertz-Makeham model to human mortality whenever feasible.

Data Availability

Life tables and age-specific population counts for Brazilian males and females in 2007 used in the analysis of the current study are available in the Dataverse repository (Missov et al., 2016): http://dx.doi.org/10.7910/DVN/BHLKA3. These datasets were derived from the following public domain resources:

http://www.ibge.gov.br/home/estatistica/populacao/tabuadevida/2007/defaulttab.shtm;

http://www.ibge.gov.br/english/estatistica/populacao/contagem2007/default.shtm.

Adjusted life tables for Brazilian males and females in 2007 used in the analysis of the current study are publicly available at http://www.lifetable.de/data/MPIDR/BRA000020072007CU1.txt, but cannot be copied according to the User Agreement at http://www.lifetable.de/useragr.htm.

All datasets from the HMD analysed during the current study are freely available at http://www.mortality.org, but cannot be “re-published in any form without the explicit permission of the data owners (usually government statistical offices)” according to the User’s Agreement at http://www.mortality.org/Public/UserAgreement.php.

The rat dataset analysed during the current study is not publicly available because of restrictions of use by the Biodemographic Database of the Max Planck Institute for Demographic Research, but is available from the corresponding author on reasonable request.

The simulated from a ΓGM datasets generated and analysed during the current study are not publicly available because of their considerable size (2,000 datasets: populations of two sizes were generated, 1,000 repetitions each), but are available from the corresponding author on reasonable request.