Abstract
We extend the classical analysis on optimal insurance design to the case when the insurer implements regulatory requirements (Value-at-Risk). Presumably, regulators impose some risk management requirement such as VaR to reduce the insurers’ insolvency risk, as well as to improve the insurance market stability. We show that VaR requirements may better protect the insured and improve economic efficiency, but have stringent negative effects on the insurance market. Our analysis reveals that the insured are better protected in the event of greater loss irrespective of the optimal design from either the insured or the insurer perspective. However, in the presence of the VaR requirement on the insurer, the insurer's insolvency risk might be increased and there are moral hazard issues in the insurance market because the optimal contract is discontinuous.
Similar content being viewed by others
Introduction
This paper shows that Value-at-Risk (VaR) regulatory requirements have controversial effects on the insurance market. On the one hand, the insured are better protected in the event of a large loss irrespective of the optimal design from either the insured's or the issuer's side, when the insurer implements VaR imposed by regulators. On the other hand, since the insurer then covers more, when a large loss occurs, the default risk of the insurer is increased, as well as the instability of the market. Moreover, because of the presence of discontinuities in the optimal insurance contract presented in this paper, the optimal risk sharing introduces moral hazard issues in the insurance market.
VaR is not a new concept in risk management. Recommendations on banking laws and regulations issued by the Basel Committee on Banking Supervision have been implemented in the banking sector. In Basel I and Basel II, the VaR methodology is used to deal with the market risk and the credit risk. Similarly, in Solvency IIFootnote 1 for the insurance sector, the economic capital could be calculated by an internal VaR model. However, whether VaR risk managementFootnote 2 requirements really enhance the efficiency and stability of the market still remains elusive. For instance, in the context of financial market, Basak and Shapiro (2001) derive that the presence of VaR risk managers amplifies the stock-market volatility in a downward market and attenuates the volatility in an upward market. The 2007–2008 global financial crises lead to even more serious concerns on the adequacy of VaR methodology to deal with credit risk. This paper reveals some negative aspects of the regulatory VaR methodology in the insurance market.
We develop a theoretical framework to investigate the economic consequences for the insured and to the insurance market in the presence of regulatory risk management requirements on insurers. This study is done under the expected utility paradigm and the risk management requirement is interpreted as a VaR constraint. The main contributions of this paper are two-fold.
First, we examine the effects on the insurance market when regulators impose a VaR constraint to the insurer. We characterize the optimal insurance contracts from the insurer's perspective to meet VaR risk management constraints. We show that the insurer's optimal insurance contract is a double-capped indemnity (Proposition 4.1). We also derive the optimal insurance contract from the insured's perspective in the presence of risk management constraints imposed on the insurer. Given the VaR constraint, the optimal contract for the insured is a capped deductible plus a deductible (Proposition 5.1). To analyze the market effects of the presence of the VaR constraint, we compare the optimal insurance contract in the presence of regulation constraints with the standard results of Arrow (1971) and Raviv (1979). We show that the insured obtain better protection in the event of higher loss and that this higher protection for large loss is compensated by a relatively lower protection against moderate loss. But, the optimal designs are discontinuous and therefore introduce moral hazard issues in the insurance market. Furthermore, the expected loss of the insurer is then higher when a large loss occurs. This leads to higher default risk of the insurer, in contrast with the purpose of reducing the default risk of the insurer by the regulatory requirement.
Second, this paper contributes to the optimal insurance design literature by adding a regulatory risk management constraint. Previous results in Arrow (1971), Raviv (1979), Cummins and Mahul (2004) and Golubin (2006) can be viewed as special cases of our results in this paper. Moreover, the technical issues associated with the non-convexity feature of the VaR constraint is tackled with the theory of “non-decreasing rearrangement”. In fact, the theory of “non-decreasing rearrangements” enables us to verify one revelation principle in our context: it suffices to consider non-decreasing indemnities only.Footnote 3
The approach of this paper is rather theoretical. An alternative is the recent empirical study by Cummins et al. (2007), which indicates that risk management contributes significantly to enhancing efficiency. Another related strand of literature emphasizes the risk management activities of the insurer, viewed as financial intermediation (e.g. Froot et al. (1993)). One objective of our paper is to compare the optimal insurance contracts ex ante and ex post the VaR risk management implementation. We do not address the issue of how insurers implement the VaR risk management system. Assuming the VaR has been appropriately implemented by the insurer, the effects on the final wealth of the insured as well as the insurer, and on the market efficiency are examined.
The remainder of this paper is organized as follows. The model is described in the next section: the optimal indemnity design problems are presented for both the insurer and the insured. The feasibility of the constraints involved in these two problems is discussed in the subsequent section. The section after that is devoted to deriving the optimal insurance contract for the insurer; the following section dwells on the optimal insurance contract for the insured. The last section provides the conclusions. All proofs are presented in the appendices.
The model
The setting is the standard framework to derive an optimal insurance contract. We consider a risk-averse insurer (endowed with non-random initial wealth w) and a representative risk-averse individual (endowed with non-random initial wealth w 0). An insurance policy, {I(x), P}, provides the reimbursement I(x) when the loss x occurs and P is the premium paid initially to the insurer. We assume that the loss x has a continuous distribution but could have a mass point at 0. The randomness of the market is represented by a probability space (Ω, Pr{ }). The expectation under Pr{ } is denoted by 𝔼[.].
Denote by c(.) the cost faced by the insurer in addition to paying the reimbursement. For the ease of exposition, c(I)=ηI, η>0.Footnote 4 The risk preference of the insurer is represented by a concave utility function V(x) defined over (0, +∞) and satisfying Inada's conditions, that is V′(0):=lim x → 0 V′(x)=+∞, V′(+∞):=lim x → ∞ V′(x)=0. The utility function of the representative insured is denoted by U(x), which is strictly concave and also satisfies Inada's conditions. The insurer's final wealth is given by

Assume that w−v is the insolvent trigger level such that whenever W<w−v the insurer is insolvent. As W<w−v is equivalent to I(x)>v+P/(1+η), to avoid the insolvency risk of the insurer, the indemnity I(x) must satisfy I(x)⩽v+P/(1+η), which means W⩾w−v. Hence, I(x)⩽v+P/(1+η) can be interpreted as a “solvency condition”. The optimal insurance design problem from the insured's perspective, under the solvency condition, is solved by Cummins and Mahul (2004). We extend the solvency condition to the case when it is satisfied with a confidence level. This amounts to setting a VaR limit on the insurer's risk management imposed, for instance, by a regulator.
Precisely, assume v is the VaR limit of the loss of time horizon T with confidence level α. Then, the final wealth of the insurer satisfies

where both v and α are introduced by regulators. We now present the optimal insurance design problems for both insurer and insured in the presence of the VaR constraint (2).
From the insurer's perspective
The optimal design problem for the insurer in the above framework is as follows:
Problem 2.1. Find an indemnity I(x) such that

The first constraint is standard (see Arrow (1971) and Raviv (1979)). Given a premium principle based on the actuarial value of the indemnity, the second constraint can be interpreted as a “premium constraint”. Indeed, similarly to Raviv (1979), we assume P=φ(𝔼[I(x)]), where φ(x) is a general strictly increasing function and φ(x)⩾x. Thus, P=φ(Δ). It is worth pointing out that our paper focuses on the optimal design and does not address the optimal premium (level). The determination of the optimal premium is often solved by fixing a premium first and next by finding an optimal premium to solve a standard maximum problem in calculus (Raviv, (1979); Schlesinger, (1981); Meyer and Ormiston, (1999)). The third constraint is the VaR constraint (2).
The last constraint prevents downward misrepresentation of the damage by the insured. This constraint is first imposed by Huberman et al. (1983), and it is used to resolve the ex post moral hazard issue. Similarly to Huberman et al. (1983), the non-decreasing assumption is imposed rather than derived from moral hazard implications or the presence of audit costs (e.g. Picard, (2000)). Furthermore, this constraint is closely related to the revelation principle (Harris et al., (1981); Myerson, (1979)): the search for an optimal indemnity schedule can be confined to the schedules under which the insured has no incentive to misrepresent the damage, which are non-decreasing indemnities only. This revelation principle in our framework is justified by the theory of “non-decreasing rearrangements” (see Carlier and Dana (2003, 2005) and Appendix B). In other words, the optimal non-decreasing indemnity of Problem 2.1 in which the last constraint is removed is the same as the optimal non-decreasing indemnity of Problem 2.1. This “non-decreasing assumption” on the indemnity plays a key role in tackling the non-convex VaR constraint (2).
From the insured's perspective
To understand the effects on the insurance market of regulators, we also consider the optimal contract design from the insured's perspective. The insurance contract is written on the aggregate loss x and we investigate the perspective of the representative insured. Under the VaR risk management constraint (2), the optimal contract design for the representative insured is the following:
Problem 2.2. Find an indemnity I(x) such that

Both Problems 2.1 and 2.2 are subject to the same constraints on I(x). As will be shown in Appendix C, a revelation principle for Problem 2.2 also holds. That is, the non-decreasing optimal indemnity of Problem 2.2 in which the last constraint is removed is the same as the optimal indemnity of Problem 2.2. We impose the “non-decreasing assumption” of the indemnity for the same reason as explained in Problem 2.1.
Previous literature
Problem 2.2 derives the optimal contract for the insured under an exogenous VaR constraint imposed by regulators on the insurer. A similar problem has recently been solved by Zhou and Wu (2008). The latter study considers a regulatory constraint on the expected tail risk instead of the probability of the tail risk. Note that a constraint on the expected shortfall is a convex-style constraint and standard techniques can be employed. We will compare the optimal contract solving Problem 2.2 with the contract in Zhou and Wu (2008) in the section “Optimal design for the insured”.
In another recent paper, Huang (2006) considers the optimal contract for the insured under the following constraint:

This constraint can be interpreted as a VaR constraint for the insured.Footnote 5 Although the problem in Huang (2006) is interesting when the insured implements VaR, we focus on the effect on the market when the insurer implements VaR. Hence we consider the policyholder's optimal contract under the insurer's VaR constraint. This difference also distinguishes our approach from that of other earlier works, such as Wang et al. (2005), Bernard and Tian (2009), in the context of the reinsurance market.
Benchmark contracts
In the absence of the VaR constraint (2), that is α=1, Problems 2.1 and 2.2 have been solved in previous literature. These standard results are summarized in Proposition 2.1 and will be used in our subsequent analysis.
Recall that a capped indemnity is a full insurance up to a capped level, written as I c(x):=min{x, c} and a deductible indemnity has the indemnification function I d (x):=max{x−d, 0}. For ease of exposition,Footnote 6 we suppose N, the largest possible loss amount of x, satisfies:

which implies that the insurer's wealth and the insured's wealth are both non-negative.
Proposition 2.1
-
Let A be a measurable subset of Ω with positive measure Pr{A}, and P be a fixed positive number. Assume

1.There exists a positive number c>0 such that the capped indemnity  solves
solves

where the cap c is determined by  Moreover
Moreover  is the unique (almost surely (a.s.)) optimal indemnity solving (5).
is the unique (almost surely (a.s.)) optimal indemnity solving (5).
2.There exists a positive number d>0 such that the deductible  solves
solves

where the deductible d is determined by  Moreover
Moreover  is the unique (a.s.) optimal indemnity solving (6).
is the unique (a.s.) optimal indemnity solving (6).
In the case of Pr{A}=1, the first part is proved by Raviv (1979) and the second part is Arrow (1971)'s deductible optimal contract. In the first part, as for the optimal design from the insurer's perspective, the second constraint in (5) means that the premium is greater than or equal to a fixed amount. This makes economic sense because the insurer requires a minimum premium to cover costs. On the other hand, the insured is willing to pay a maximum upfront premium (see the second constraint in (6)). In our subsequent applications, the constraint 𝔼[I(x) A
]=Δ is often considered. This proposition also follows from the results by Golubin (2006) for Pr{A}=1. When 0<Pr{A}<1, the proof is similar, by restricting the space probability to the states of nature in the set A, and could be obtained from the authors upon request.
A
]=Δ is often considered. This proposition also follows from the results by Golubin (2006) for Pr{A}=1. When 0<Pr{A}<1, the proof is similar, by restricting the space probability to the states of nature in the set A, and could be obtained from the authors upon request.
Feasible constraints in Problems 2.1 and 2.2
Before solving Problems 2.1 and 2.2 in the next two sections, we need to discuss the feasibility of the constraints first. The purpose of this section is to clarify the set of feasible constraints among {Δ, v, α}. In the remainder of this paper, we fix a=(P+v)/(1+η) and q is the (1−α) quantile of x, that is Pr{x⩽q}=1−α.
The first auxiliary problem solves for the possible range of the VaR parameters {v, α} when the actuarial value Δ is given.
Problem 3.1. Solve the optimal indemnity I(x) such that

Problem 3.1 solves the maximum probability of the event that the indemnity I(x) is less than a if a minimal actuarial value Δ is guaranteed. This formulation does not depend on the premium principle, but if the premium principle is used, it turns out that Problem 1 determines the maximum survival probability of the insurerFootnote 7 when a minimum premium is charged upfront. The solution of Problem 3.1 is presented in the next proposition.
Proposition 3.1.
-
Define a function Δ min (.) by

and Δ min =Δ min (a).
-
1
If Δ<Δ min , the maximum survival probability in Problem 3.1 is 1, and any indemnity I c(x) with c⩽a and 𝔼[I c(x)]⩾Δ is optimal for Problem 3.1.
-
2
If Δ min ⩽Δ<𝔼[x], then there exists a positive λ⩾a such that the non-decreasing coverage (Figure 1):

is optimal, where λ is determined by solving the 𝔼[J a,λ (x)]=Δ. Moreover, among the non-decreasing optimal indemnities, J a,λ (x) is unique a.s.
-
1
Proof. See Appendix A.□
The second auxiliary problem is the dual to Problem 3.1. It solves for the range of the actuarial value Δ when the VaR constraint (2) is imposed.
Problem 3.2. Solve for the indemnity I(x)

As the premium is based on the actuarial value, Problem 3.2 is the same as the expected utility for a risk-neutral insured, under the insurer's VaR constraint (2). Problem 3.2 is different from the risk-neutral insured's expected utility problem under the insured's VaR constraint, considered in Wang et al. (2005) and Bernard and Tian (2009).Footnote 8
Proposition 3.2.
-
-
1
If Pr{x>a}<α, or equivalently, q⩽a, then Pr{I(x)>a}<α since I(x)⩽x. Therefore the full insurance I(x)=x solves Problem 3.2.
-
2
If 0<α⩽Pr{x>a}, or equivalently a<q, then the coverage J a,q (X) solves Problem 3.2. Moreover, any non-decreasing optimal indemnity of Problem 3.2 is J a,q (x) a.s.
-
1
Proof. See Appendix A. □
Let Δ max :=𝔼[J a,q (x)]. According to Proposition 3.2, Δ max is the maximum possible actuarial value of the indemnity. Hence, to make both Problems 2.1 and 2.2 feasible, we assume

Optimal design for the insurer
This section presents the optimal design for the risk-averse insurer subject to VaR regulation rules and compares with Raviv's (1979) classical capped indemnity in the absence of the VaR constraint.
For the ease of exposition of the optimal design of the insurer and the insured (in the next section), we term a double-capped indemnity as  where c
1, c
2, q >0. A double-deductible indemnity is defined as
where c
1, c
2, q >0. A double-deductible indemnity is defined as 
 for positive numbers d
1, d
2 and q. A capped deductible indemnity has the form of min{c, I
d
(x)} for positive numbers c and d.
for positive numbers d
1, d
2 and q. A capped deductible indemnity has the form of min{c, I
d
(x)} for positive numbers c and d.
To solve Problem 2.1, we first consider the following problem.
Problem 4.1.

Then, Problem 2.1 is easily solved after characterizing the optimal indemnity of Problem 4.1 for a general probability parameter α. Later we will rationalize this approach because the VaR Constraint (2) is not necessarily binding in Problem 2.1.
Proposition 4.1.
-
For any 0<Δ⩽Δ max , a<q, where q is the (1−α) quantile of x,
-
1
If Δ⩽Δ min , then there exists a positive c⩽a such that the capped indemnity I c(x) is the optimal indemnity of Problem 2.1.
-
2
If Δ min <Δ⩽Δ max , then there exists a positive c>a such that the double-capped indemnity I a(x)
 x⩽q
+I
c(x)
x⩽q
+I
c(x) x>q
is the optimal indemnity of Problem 4.1. Moreover, the non-decreasing optimal indemnity of Problem 4.1 is unique a.s. If Δ=Δ
max
, this is in fact J
a,q
(x).
x>q
is the optimal indemnity of Problem 4.1. Moreover, the non-decreasing optimal indemnity of Problem 4.1 is unique a.s. If Δ=Δ
max
, this is in fact J
a,q
(x).
-
1
Proof. The first part of this proposition follows from Proposition 1 easily. If Δ⩽Δ min , then there exists a positive c⩽a such that Δ=Δ min (c). Hence by Proposition 2.1, the capped indemnity I c(x) is the optimal indemnity subject to the premium constraint that E[I(x)]=Δ. Clearly I c(x) is also optimal to Problem 2.1 since Pr{W<w−v}=0 and the VaR constraint is redundant. For the second part, see Appendix B. □
The proof of the second part of Proposition 4.1 is quite complicated. We explain briefly the main ideas. The proof is divided into three steps. The first step verifies the revelation principle: it suffices to consider non-decreasing indemnities I(x) only. This step makes use of “non-decreasing rearrangements”. In the second step, by considering non-decreasing indemnities only, the optimal indemnity of Problem 4.1 is characterized as a double-capped indemnity  The last step is the most technical one. We show that the first cap level c
1 in the optimal indemnity is equal to a. Thus, there is only one unknown parameter, the second cap level c, which is determined by the actuarial value 𝔼[I(x)]=Δ. When Δ=Δ
max
, the result is consistent with Proposition 3.2.
The last step is the most technical one. We show that the first cap level c
1 in the optimal indemnity is equal to a. Thus, there is only one unknown parameter, the second cap level c, which is determined by the actuarial value 𝔼[I(x)]=Δ. When Δ=Δ
max
, the result is consistent with Proposition 3.2.
The optimal indemnity of Problem 4.1 can be written as a combination of some simple indemnities. If the second cap c⩽q, the optimal indemnity can be written as I
a(x)+(c−a) x>q
, a capped indemnity plus an indemnity that pays a constant amount c−a only when the loss amount x is (strictly) greater than a.Footnote 9 This indemnity is called a “digital indemnity” since it corresponds to a digital option contract in the financial market. If c>q, there are three components in the optimal contract. The first one is the capped indemnity I
a(x), the second one is a digital indemnity (q−a)
x>q
, a capped indemnity plus an indemnity that pays a constant amount c−a only when the loss amount x is (strictly) greater than a.Footnote 9 This indemnity is called a “digital indemnity” since it corresponds to a digital option contract in the financial market. If c>q, there are three components in the optimal contract. The first one is the capped indemnity I
a(x), the second one is a digital indemnity (q−a) x>q
, while the last one is a capped deductible indemnity with deductible q and cap level c−q. In the presence of the digital indemnity, both insurer and insured are willing and able to shift the reimbursements from moderate to the large level of loss. If this kind of digital indemnity is absent, there are not enough (Arrow-Debreu) securities to build the optimal policy. In the next section, we derive the same results from the insured's perspective as well.
x>q
, while the last one is a capped deductible indemnity with deductible q and cap level c−q. In the presence of the digital indemnity, both insurer and insured are willing and able to shift the reimbursements from moderate to the large level of loss. If this kind of digital indemnity is absent, there are not enough (Arrow-Debreu) securities to build the optimal policy. In the next section, we derive the same results from the insured's perspective as well.
A remarkable feature in the optimal design is its discontinuous-indemnity ingredient in the event {x>q}. This discontinuous ingredient is pervasive in the optimal design when a probability constraint is involved, and it appeared also in Bernard and Tian (2009), Gollier (1987), Gajek and Zagrodny (2004) and in Propositions 3.1 and 3.2 of the last section. The presence of a discontinuity introduces moral hazard: if the loss is slightly lower than the threshold, it is optimal for the insured to increase the loss. It thus gives incentives of the insured to manipulate the actual loss.Footnote 10
According to Proposition 4.1, the non-decreasing optimal indemnity of Problem 4.1 is unique. This uniqueness result is somewhat surprising. The subtle issue is the non-convex style constraint Pr{W<w−v}=α. Hence, there are no available standard results about the existence and the uniqueness when the constraint is non-convex (see Luenberger, (1971)).
We now study how the second cap level c depends on α, or, equivalently, q. To emphasize this dependence, we express c=c(q) by treating q as a variable. Let g(x) denote the density function of the loss variable. From Proposition 4.1, we obtain that if c(q)⩾q,

By differentiating the last equation with respect to the argument q, we obtain

In particular, c′(q)>0 and c(q) is increasing with respect to q. Moreover, lim q↓a c(q)=c *, such that 𝔼[I c*(x)]=Δ. As Δ>Δ min , we have c *>a. Hence, c(q), in the region {c(q)⩾q}, is determined by Equation (11) and the initial boundary condition that c(a)=c *.
To finish the characterization of the function c(q) for all possible parameter q, we consider the region in which c(q)⩽q. From the earlier discussion, it might occur when the curve c=c(q) meets the curve c=q at q * in the (q,c)-space. If c(q)⩽q, then by Proposition 4.1,

By differentiating with respect to q, we obtain

In particular, c(q) is strictly increasing. Hence c(q), over the region c(q)⩽q, is determined by Equation (13) and a suitable initial boundary condition.
We are now able to solve Problem 2.1.
Owing to the uniqueness result in Proposition 4.1, we use Ĩ α to denote the unique (a.s.) non-decreasing indemnity in Proposition 4.1 for a corresponding parameter α. The next proposition presents the optimal indemnity of Problem 2.1. To highlight the dependence on the probability level α, we employ notation Δ max (α) instead of Δ max . Therefore Δ max (α)=𝔼[J a,qα ], where q α is the (1−α) quantile of x. As a function of the argument α, Δ max (α) is non-decreasing.
Proposition 4.2. Assume Δ
min
<Δ<Δ
max
(α). Let α
0 satisfy Δ
max
(α
0)=Δ. For any α
1∈[α
0,α], there exists a non-decreasing indemnity  solving Problem 4.1, where α is replaced by α
1. Let
solving Problem 4.1, where α is replaced by α
1. Let

Then  is an optimal solution of Problem 2.1. Moreover, any non-decreasing optimal solution of Problem 2.1 must be a double-capped indemnity.
is an optimal solution of Problem 2.1. Moreover, any non-decreasing optimal solution of Problem 2.1 must be a double-capped indemnity.
This proposition follows from Proposition 4.1 easily. By continuity arguments and monotonicity of the function Δ max (β) with respect to the argument β, there exists α 0∈[0,α], such that Δ max (α 0)=Δ. The existence of α̂ is also evident using a continuity argument.
Note that α is the confidence level defined in the VaR constraint (2) and α
0 is determined by the actuarial value Δ. The VaR constraint is binding if and only if α̂=α. In contrast with the convex-style constraint problem, however, the VaR constraint (2) is not necessarily binding. To see this point, we write  and consider the first-order derivative with respect to q
α1, the (1−α
1)-quantile of x. By abuse of notation, we make use of α and q instead of α
1 and q
α
1. By straightforward computation, we have
and consider the first-order derivative with respect to q
α1, the (1−α
1)-quantile of x. By abuse of notation, we make use of α and q instead of α
1 and q
α
1. By straightforward computation, we have

Since a<q, V(w+Δ−(1+η)a)>V(w+Δ−(1+η)q)}. However, since V(.) is increasing and using (11) and (13), V′(w+P−(1+η)c(q))c′(q) × ∫N
min{c(q),q}g(x)dx>0. Therefore  (.) is not necessarily monotonic with respect to q by formula (14). Consequently,
(.) is not necessarily monotonic with respect to q by formula (14). Consequently,  (α1) is not necessarily monotonic with respect to α
1. This means that VaR constraint (2) is not necessarily binding in Proposition 4.2. This point is remarkable as we have to reduce Problem 2.1 to solving a sequence of Problem 4.1 as outlined above. This point, however, is overlooked in Huang (2006). We present some numerical examples in the next section for this important point.
(α1) is not necessarily monotonic with respect to α
1. This means that VaR constraint (2) is not necessarily binding in Proposition 4.2. This point is remarkable as we have to reduce Problem 2.1 to solving a sequence of Problem 4.1 as outlined above. This point, however, is overlooked in Huang (2006). We present some numerical examples in the next section for this important point.
Numerical examples
By way of example, we plot several graphs of the function  (α
1) in Panel A–Panel D of Figure 2. These four graphs clearly show that the function
(α
1) in Panel A–Panel D of Figure 2. These four graphs clearly show that the function  (α
1) is not monotonic. Hence the VaR constraint is not necessarily binding for the optimal contract of Problem 2.1.
(α
1) is not monotonic. Hence the VaR constraint is not necessarily binding for the optimal contract of Problem 2.1.
Function T(α)In these graphs, w=10, V(x)=x 1−γ/1−γ, with γ=3, η=0.05 and α=0.1. The loss x follows either a truncated normal distribution11 over [0,8] (see Panel A) or a uniform distribution over [0,8] (see panels B–D). In panel A, X is a truncated normal N(4,6) with P=42, v=2, Δ=3.8532, Δ min =3.75, Δ max (α)=3.91, a=5.90, q α =7.1 and α min =0.058. In panels B–D, X is uniformly distributed over [0,8]. In panel B, P=4.3, v=2, Δ=3.83, Δ min =3.75, Δ max (α)=3.91, a=6, q α =7.2 and α min =0.044. In panel C, P=4.1, v=2, Δ=3.73, Δ min =3.70, Δ max (α)=3.88, a=5.81, q α =7.2 and α min =0.014. In panel D, P=4.4, v=3, Δ=3.97, Δ min =3.94, Δ max (α)=4.00, a=7.04, q α =7.2 and α min =0.034. Our purpose is to show that the shape of (α) is rich: increasing, decreasing, hump or other complicated functions.Footnote
12 The risk management constraint imposed on the insurer is very different from imposing a risk management constraint to the insured (as in Huang, (2006)). In the latter case the insured does not have to take into consideration the insurer's interests. We argue that the VaR constraint to the insurer is important because insurers are regulated while insured are often not (except in the reinsurance market, as the insured are insurance companies).
Analysis
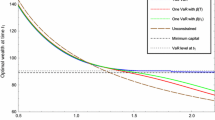
The explicit optimal design derived in the previous section enables us to compare with Raviv's (1979) optimal design without VaR constraint. To illustrate this comparison, we consider two identical insurance companies while one implements the VaR policy that Pr{W<w−v}⩽α and another does not. We consider the impacts to the insurer and the insured separately. For this purpose we assume the same premium P is paid and the insurance contracts are issued based on the optimal design by Proposition 4.1 and Proposition 2.1, respectively. Let a and c be the cap levels of the double-capped indemnity in Proposition 4.1 and r be the cap level in Raviv's indemnity. Clearly, a<r<c because both contracts have the same actuarial value. Both panel A and panel B in Figure 3 show the comparisons between the optimal insurance contract with risk management consideration and Raviv's (1979) capped indemnity without risk management consideration. In panel A the second cap c>q, and c⩽q in Panel B.
From Figure 3, both companies provide full insurance for insured when the loss x⩽a. If the moderate loss of x occurs, say a⩽x⩽q, Raviv's optimal contract provides higher protection for the insured. In the event of a high loss of x>q, the insurance company that follows the risk management policy actually provides better protection to the insured. Higher protection for extreme loss looks more attractive for risk-averse insurance buyers.
On the other hand, from the insurer's perspective, Raviv's optimal insurance is not acceptable because it would violate regulatory requirements. To meet the VaR requirement, the insurer has to provide relatively higher indemnity protection when an extreme loss occurs, and consequently, to provide less protection if the loss x occurs in a moderate level a⩽x⩽q. The digital indemnity improves the risk-sharing mechanism, and it enables to shift the indemnity from a moderate level of loss to the coverage of large losses. However, the presence of the discontinuity in the design induces moral hazard: The insured have incentive to inflate losses when it is slightly below q. Moreover, if insurers offer this type of indemnities, then their expected loss in case a loss occurs is greater. It thus increases the default risk of the insurer, which is opposite to the regulatory requirement to reduce the default risk of the insurer. Hence, there is a trade-off between the insured and the insurer and the VaR efffect on the insurance market as a whole is controversial. We will observe the same discoveries for the optimal contract from the insured's perspective in the next section.
Optimal design for insured
The previous section presents the optimal insurance design for the insurer. In this section, we discuss the optimal insurance design for the insured in the presence of the insurer's risk management policies. In the presence of a risk management constraint, Arrow's (1971) deductible policy might not be available because it does not meet the VaR requirement for the insurer. Therefore, the risk management constraint for the insurer indirectly influences the optimal design for the insured.Footnote 12
Similar to Section 4, we reduce Problem 2.2 to Problem 5.1, where α is a generic probability parameter.
Problem 5.1. Find the indemnity I such that:

The next proposition explicitly characterizes the optimal non-decreasing indemnity for the insured in Problem 5.1,and consequently,solves Problem 2.2.
Proposition 5.1
-
For any 0⩽Δ⩽Δ max , a<q, where q is the 1−α quantile of x. Define

-
1
If Δ⩽
 (q), then there exists a positive d⩾q−a such that the deductible indemnity I
d
(x) is the optimal indemnity of Problem 2.2. The Var constraint is redundant.
(q), then there exists a positive d⩾q−a such that the deductible indemnity I
d
(x) is the optimal indemnity of Problem 2.2. The Var constraint is redundant. -
2
If
 (q)<Δ⩽Δ
max
, then the unique non-decreasing optimal indemnity I
* of Problem 5.1 is written as
(q)<Δ⩽Δ
max
, then the unique non-decreasing optimal indemnity I
* of Problem 5.1 is written as 
where d * satisfies 𝔼[I *(x)]=Δ. Moreover, d*⩽q−a. If Δ=Δ max (α), I *(x)=J a,q (x)
Proof. The first part of Proposition 5.1 follows from Proposition 2.1 [1]: when Δ⩽M(q), there exists a unique d⩾q−a such that Δ=𝔼[(x−d)+]. For the remaining proof of this proposition, refer to Appendix C. □
The second part of Proposition 5.1 presents the optimal insurance design for the insured under the insurer's risk management constraint. A complete proof is fairly lengthy and technical (See Appendix C for details). Thus it is helpful to explain intuitions of the proof. Similar to the proof of Proposition 4.1, there are three steps. In the first step, we verify the revelation principle, and so confine ourselves to non-decreasing indemnities. The second step is to characterize the optimal design as  The last step is to prove that one particular indemnity is optimal. Namely, d
1=d
2 in the optimal indemnity contract. When Δ=Δ
max
, the result is consistent with Proposition 3.2.
The last step is to prove that one particular indemnity is optimal. Namely, d
1=d
2 in the optimal indemnity contract. When Δ=Δ
max
, the result is consistent with Proposition 3.2.
Similar to the last section, the sensitivity of d * with respect to q can be derived explicitly by using Proposition 5.1. However, VaR constraint (2) is not necessarily binding and hence the solution of Problem 2.2 must be derived by a similar procedure as that in Proposition 4.2.Footnote 13
In the special case α=0, q
α
=∞, and the probability constraint Pr{W<w−v}=α is reduced to I(x)⩽a, a.s. Then, the optimal indemnity is min which has been proved by Cummins and Mahul (2004). In the next subsection, we compare the optimal indemnity in Proposition 5.1 with Arrow's deductible contract.
which has been proved by Cummins and Mahul (2004). In the next subsection, we compare the optimal indemnity in Proposition 5.1 with Arrow's deductible contract.
Analysis
Similar to the analysis in the previous section, we consider two identical companies: one that implements the VaR policy and the other that does not. A risk-averse insured buys insurance from both insurance companies by paying the same policy premium. One optimal insurance contract is Arrow's deductible contract with deductible level d
arrow(x), whereas the other optimal insurance contract, by Proposition 5.1, is I
*(x)=min{a, I
d*
(x)} x⩽q
+I
d*
(x)
x⩽q
+I
d*
(x) x>q
for some q and d
*.
x>q
for some q and d
*.
Figure 4 displays both optimal insurance contracts. As both contracts have the same actuarial value, d
*<d
arrow for any loss distribution of x. Consequently, when d
*⩽x⩽d
arrow+a or x>q, we have  This feature is similar to the optimal design from the perspective of the insurer. Moreover, to compensate the higher protection in the event of higher loss, the insured are willing to receive reduced indemnity in the event of moderate level of loss. Again, the digital indemnity allows an efficient risk-sharing. The protection amount is shifted from moderate level of loss to higher level of loss. Without digital indemnities, there exists no optimal insurance contract if the insurer follows the VaR constraint. Therefore, the presence of the digital indemnity improves the market efficiency by enhancing risk-sharing opportunities.
This feature is similar to the optimal design from the perspective of the insurer. Moreover, to compensate the higher protection in the event of higher loss, the insured are willing to receive reduced indemnity in the event of moderate level of loss. Again, the digital indemnity allows an efficient risk-sharing. The protection amount is shifted from moderate level of loss to higher level of loss. Without digital indemnities, there exists no optimal insurance contract if the insurer follows the VaR constraint. Therefore, the presence of the digital indemnity improves the market efficiency by enhancing risk-sharing opportunities.
Similar to the last section, the insured is better protected in the event of a higher loss because of the VaR requirement on the insurer. In a sense, the VaR requirement has positive effects on the insured as it offers better protection to the insured as desired by insurance regulators. However, it might increase the default risk of the insurer as the amount of loss for the insurer in case of an insurance claim is higher. The smaller the d *, the larger the extra loss d Arrow−d * over the classical deductible contract. Moral hazard is another issue because of the discontinuity of the optimal contract.
These effects are very specific to VaR requirements. As shown in Zhou and Wu (2008), for instance, when the insurer implements the expected shortfall requirements, the insured's optimal indemnity is a capped deductible (clearly, it is continuous).Footnote 14 The expected shortfall requirement might be attractive for the insurer, as the indemnity is capped. However, from the insured's perspective, the default risk is increased. Therefore, different regulatory risk management has shown various effects on the insured and on the insurer.
Conclusions
We present a theoretical framework to examine the effects of VaR constraints imposed by regulators on insurers, on the optimal form of insurance contracting. When the insurer follows the VaR metric, the optimal insurance designs from both the insurer and the insured's perspectives are derived explicitly. In the optimal insurance designs, the insured is always better protected in the event of a larger loss. This suggests that the risk management constraint enhances the final wealth of risk-averse insured in the event of a higher loss. Nevertheless, VaR regulation creates moral hazard and increases the default risk of the insurer when large losses occur. According to our results, VaR methodology might not naturally address the risk management of the insurance market.
Notes
Solvency II is a new regulatory capital framework for insurance companies initiated by the European Union and starting to be developed in Northern America. We refer to EFMA's report (2006) for its current stage.
Our regulatory risk management is different from the regulatory constraints considered in Raviv (1979). Raviv's description of the regulatory constraint is based on Joskow (1973) and Peltzman (1976). In those works, regulation is endogenous, but current regulation becomes compulsory.
The non-decreasing rearrangement concept was first introduced to the insurance literature by Carlier and Dana (2003, 2005).
The method could easily be applied to more general function forms of the cost function, where the function C(.) defined by C(t)=t+c(t) is non-decreasing, differentiable over [0, N], and C is invertible.
Note that Pr{W i⩾𝔼[W i]−v}=Pr{W i ⩾w 0−v 0}, where v 0=v+P+𝔼[x]−Δ.
It is possible to accept negative wealth by taking some more general utility functions defined on (a,+∞) for a negative number a.
Recall that I(x)>a is equivalent to W<w−v.
Let I *(x) denote the optimal solution of the corresponding problem of Problem 3.2 under the VaR constraint of the insured. Then I *(x) has the form (x−d)+
 x
⩽
q
as shown in Wang et al. (2005) and Bernard and Tian (2009). Hence the net loss x−I
*(x) has the same shape as J
a,
λ
. We refer to Bernard and Tian (2009) for more details.
x
⩽
q
as shown in Wang et al. (2005) and Bernard and Tian (2009). Hence the net loss x−I
*(x) has the same shape as J
a,
λ
. We refer to Bernard and Tian (2009) for more details.In the sense of probability, there is no difference between x>a and x⩾a.
Implementing discontinuous indemnities is not easy in practice. One way to resolve this moral hazard issue is to impose another constraint, that the retention x−I(x) is non-decreasing. Combining the non-decreasing assumption of I(x), we see that I(x) is 1-Lipschitz and hence continuous. We refer to Huberman et al. (1983) and Carlier and Dana (2003) for more discussions on non-decreasing retentions.
12 The risk management constraint imposed on the insurer is very different from imposing a risk management constraint to the insured (as in Huang, (2006)). In the latter case the insured does not have to take into consideration the insurer's interests. We argue that the VaR constraint to the insurer is important because insurers are regulated while insured are often not (except in the reinsurance market, as the insured are insurance companies).
13 We omit the details, which are available from the authors upon request.
14 Other extensions to general convex risk measure constraints have been investigated by Ludkowski and Young (2008).
11 The density of a truncated normal N(m,σ) is given by

References
Arrow, K. (1971) Essays in the Theory of Risk Bearing, Chicago: Markham.
Basak, S. and Shapiro, A. (2001) ‘Value-at-risk-based risk management: Optimal policies and asset prices’, Review of Financial Studies 14 (2): 371–405.
Bernard, C. and Tian, W. (2009) ‘Optimal reinsurance arrangements under tail risk measures’, Journal of Risk and Insurance, 76 (3), 709–725.
Carlier, G. and Dana, R.-A. (2003) ‘Pareto efficient insurance contracts when the insurer's cost function is discontinuous’, Economic Theory 21 (4): 871–893.
Carlier, G. and Dana, R.-A. (2005) ‘Rearrangement inequalities in non-convex insurance models’, Journal of Mathematical Economics 41 (4–5): 483–503.
Cummins, J., Dionne, G., Gagné, R. and Nouira, A. (2007) ‘Efficiency of insurance firms with endogenous risk management and financial intermediation activities’, Working paper presented at the ARIA 2007 annual meeting.
Cummins, J. and Mahul, O. (2004) ‘The demand for insurance with an upper limit on coverage’, Journal of Risk and Insurance 71 (2): 253–264.
EFMA (2006) ‘Risk management in the insurance industry and solvency II: European survey’, Capgemini Consulting, http://capegimini.com/resources/thought_leadership/risk_management_ in_the_insurance_industry_and_salvency_ii/.
Froot, K., Scharfstein, D. and Stein, J. (1993) ‘Risk management: Coordinating corporate investment and financing policies’, Journal of Finance 48 (5): 1629–1658.
Gajek, L. and Zagrodny, D. (2004) ‘Reinsurance arrangements maximizing insurer's survival probability’, Journal of Risk and Insurance 71 (3): 421–435.
Gollier, C. (1987) ‘Pareto-optimal risk sharing with fixed costs per claim’, Scandinavian Actuarial Journal 13: 62–73.
Golubin, A. (2006) ‘Pareto-optimal insurance policies in the models with a premium based on the actuarial value’, Journal of Risk and Insurance 73 (3): 469–487.
Harris, M., Townsend, R.M. and Smith, C. (1981) ‘Resource allocation under asymmetric information’, Econometrica 49: 33–64.
Huang, H.-H. (2006) ‘Optimal insurance design under a value-at-risk constraint’, The Geneva Risk and Insurance Review 31 (2): 91–110.
Huberman, G., Mayes, D. and Smith, C. (1983) ‘Optimal insurance policy indemnity schedules’, Bell Journal of Economics 14 (2): 415–426.
Joskow, P.L. (1973) ‘Cartels, competitions and regulation in the property-liability insurance industry’, Bell Journal of Economics and Management Science 4 (2): 375–427.
Ludkowski, M. and Young, V.R. (2008) ‘Optimal risk sharing under distorted probabilities’, Working paper.
Luenberger, D. (1971) Optimization by Vector Space Methods, Wiley Professional Paperback Series.
Meyer, J. and Ormiston, M. (1999) ‘Analyzing the demand for deductible insurance’, Journal of Risk and Uncertainty 18 (3): 223–230.
Myerson, R. (1979) ‘Incentive compatibility and the bargaining problem’, Econometrica 47: 61–74.
Peltzman, S. (1976) ‘Toward a more general theory of regulation’, Journal of Law and Economics 19 (2): 211–246.
Picard, P. (2000) ‘On the design of optimal insurance policies under manipulation of audit cost’, International Economic Review 41 (4): 1049–1071.
Raviv, A. (1979) ‘The design of an optimal insurance policy’, American Economic Review 69 (1): 84–96.
Schlesinger, H. (1981) ‘The optimal level of deductibility in insurance contract’, Journal of Risk and Insurance 48 (3): 465–481.
Wang, C.P., Shyu, D. and Huang, H.-H. (2005) ‘Optimal insurance design under a value-at-risk framework arrangements’, Geneva Risk and Insurance Review 30: 161–179.
Zhou, C. and Wu, C. (2008) ‘Optimal insurance under the insurer's risk constraint’, Insurance: Mathematics and Economics 42: 992–999.
Acknowledgements
C. Bernard gratefully acknowledges financial support from the Natural Sciences and Engineering Research Council of Canada. We thank the editor and two anonymous referees for their constructive comments that improved the paper. Thanks are also due to Phelim Boyle, Pierre Devolder, Georges Dionne, Harry Panjer, Antoon Pelsserr and participants at the 2008 ARIA meeting in Portland, the workshop Finance, Stochastics, Insurance in February 2008 in Bonn, the seminars at the School of Economics in Amsterdam, the CORE in Louvain-la-Neuve, Belgium, and the Department of Economics at the University of Guelph.
Author information
Authors and Affiliations
Appendices
Appendix A
Proof in Section 3: Constraints Feasibility
Proof of proposition 3.1
We only provide a detailed proof of the second part, which requires the following two lemmas.
Lemma A.1. If Y * satisfies the following three properties:
-
1
0⩽Y *⩽x,
-
2
𝔼[Y *]=Δ,
-
3
there exists a positive λ>0 such that for each ω∈Ω, Y *(ω) is a solution of the following optimization problem:

then Y * solves the optimization problem 3.1.
Proof. Given a coverage I that satisfies the constraints of the optimization problem 3.1, using (iii), we have

Thus,  After taking the expectation, and using condition (ii) one obtains
After taking the expectation, and using condition (ii) one obtains

Therefore, applying the constraints on I, 𝔼[I(x)]⩾Δ, Pr{Y *⩽a}⩾Pr{I⩽a}. The proof of this lemma is completed. □
Lemma A.2. For each λ>0, the indemnity J a,a+1/λ (defined by (8) and graphically represented in Figure 1 ) satisfies conditions (i) and (iii) of Lemma A.1.
Proof. Property (i) is obviously satisfied. To check property (iii), we first note that when x⩽a, the objective function is 1+λy for 0⩽y⩽x. Hence x is the maximum point in this subregion {x⩽a}. When x>a, consider two regions of y separately. In the region y∈[0, a], the maximum value of the function  y⩽a
+λ
y is 1+λa at local maximum point a. On the other hand, in the region y∈(a, x], the maximum value of the objective function 1
y⩽a
+λy becomes λx at the local maximum point x. Thus, if λx>1+λa, or equivalently, x>a+1/λ, x is the global maximum point; otherwise, a is the global maximum point. Lemma A.2 is proved. □
y⩽a
+λ
y is 1+λa at local maximum point a. On the other hand, in the region y∈(a, x], the maximum value of the objective function 1
y⩽a
+λy becomes λx at the local maximum point x. Thus, if λx>1+λa, or equivalently, x>a+1/λ, x is the global maximum point; otherwise, a is the global maximum point. Lemma A.2 is proved. □
Proof of Proposition 3.1. According to Lemmas A.1 and A.2, it suffices to prove the existence of λ *>0 such that J a,a+1/λ* satisfies condition (ii) of Lemma A.1. We compute the expectation of J a,a+1/λ : ɛ λ := 𝔼[J a,a+1/λ ]. We have

The existence of a solution λ *>0 such that ɛ λ =Δ comes from the assumption on the continuous distribution of x and thus the continuity of function ɛ λ of the variable λ.
We now prove that the optimal solution is unique a.s. among the non-decreasing functions of the loss amount x. Let I(x) be another optimal non-decreasing indemnity of Problem 3.1 and I *=J a,a+1/λ* . We prove that I(x)=I *(x) a.s. In fact, by construction,

As I(.) and I
*(.) are both non-decreasing, there exist two positive numbers A and A* such that {I(x)⩽a} = {x⩽A} and {I
*(x)⩽a} = {x⩽A
*}. As I and I
* are both optimal, Pr{I(x)⩽a} = Pr{I*(x)⩽a}. Then Pr{x⩽A} = Pr{x⩽A*}. As X has a continuous distribution function, one obtains A=A
*. Thus,  I(x)⩽a
=
I(x)⩽a
=  I*(x)⩽a
a.s. Consequently, using (A1) and λ
*>0,
I*(x)⩽a
a.s. Consequently, using (A1) and λ
*>0,

As 𝔼[I *−I] = 0 and I *−I⩾0 a.s., one obtains I = I * a.s. Proposition 3.1 is proved. □
Proof of Proposition 3.2. The proof is similar to the proof of Proposition 3.1. It is straightforward to see that the indemnity J a,a+λ (x(ω)) solves the static optimization problem below, for each λ>0 and for all ω,

By using the binding VaR constraint, the optimal λ * satisfies a+λ *=q. Thus J a,q (x) is the optimal design. The uniqueness of the optimal design is also similar. □
Appendix B
Proof of Proposition 1: Optimal design for the insurer
We first recall the definition of the “non-decreasing rearrangement” and its key properties (see Carlier and Dana (2005), Proposition 1). Let μ x be the associated Borel measure on [0, N] of the loss variable x. By assumption on the continuous distribution of x, μ x is a nonatomic Borel measure.
Definition B.1. Given a μ x -Borel function f:[0,N] → [0,N], there exists a unique (up to μ x −a.e equivalence) non-decreasing function f̃ that is equimeasurable to f with respect to μ x . Moreover, f̃(t)=inf{u:v(u)⩾t}, where

f̃ is called the non-decreasing rearrangement of f. As f and f̃ are equimeasurable with respect to μ x , for all measurable function g(.),

Moreover, a variant of Hardy–Littlewood inequality holds. Precisely, if L(x,t) : [0,N]2 → ℝ is  1 such that for all t∈[0,N] the function x → ∂L/∂t(x,t) is increasing, then
1 such that for all t∈[0,N] the function x → ∂L/∂t(x,t) is increasing, then

In the following discussion, given an indemnity form I(.) : [0,N] → [0,N], there exists a non-decreasing rearrangement of I(.) that is equimeasurable to I(.), with respect to μ x . If 0⩽I(x)⩽x, then by the proof in Carlier and Dana (2005), Lemma 2, we obtain 0⩽Ĩ(x)⩽x.
The next lemma justifies the revelation principle in the current VaR framework. Moreover, it shows us that the optimal non-decreasing indemnity is a double-capped indemnity.
Lemma B.1. If there exists an optimal solution I* to Problem 4.1, then there exists a non-decreasing optimal indemnity Ĩ* to Problem 4.1. Moreover, any optimal non-decreasing solution of Problem 1 is a double-capped indemnity as follows:

where c 1⩾0 and c 2⩾0. Furthermore, c 1⩽a⩽c 2.
Proof. Given an optimal indemnity I *(.), denote by Ĩ*(.) the non-decreasing rearrangement of I *. Clearly, Ĩ* is also an optimal solution of Problem 4.1. Indeed it satisfies every constraint of Problem 4.1:

Moreover, because of the equi-measurability of I *(x) and its non-decreasing rearrangement Ĩ*(x), we have

Thus Ĩ*(x) is also optimal. The first part of this lemma has been proved.
We then prove that any non-decreasing optimal solution of Problem 4.1 is a double-capped indemnity. Assume Ĩ* is a non-decreasing optimal solution of Problem 4.1. Then there exist Ω1 and Ω2 such that
-
Ω1 = {Ĩ*⩽a} and Ω1 = {Ĩ*>a},
-
Ω1∩Ω2 = ∅,Ω1∪Ω2 = Ω,
-
Pr{Ω1} = 1−α and Pr{Ω2} = α.
As Ĩ* is non-decreasing with respect to x, there exists a constant A such that Ω1 = {x⩽A} and Ω2 = {x>A}. Recall that q is the (1−α) quantile of the distribution of x. As x is continuously distributed, Pr{Ω2} = α implies that q = A. Thus:

Define Ĩ* 1 and Ĩ* 2 by

and Δ1 and Δ2 such that

Let J 1 * and J 2 * be

where J i , I=1, 2 respectively, solves the following optimization problem:

By Proposition 2.1, there exist c 1, c 2⩾0 such that

where c
1 and c
2 satisfy 
for i=1, 2.
Claim. c 1⩽a<c 2.
Proof of the claim. In fact, 𝔼[Ĩ*(x) x≤q
]=Δ1. As {x⩽q}={Ĩ*(x)⩽a}, the indemnity Ĩ
1
*(x) stays in the range [0, min(x, a)] over the region {x⩽q}. Then Δ1⩽𝔼[I
a(x)
x≤q
]=Δ1. As {x⩽q}={Ĩ*(x)⩽a}, the indemnity Ĩ
1
*(x) stays in the range [0, min(x, a)] over the region {x⩽q}. Then Δ1⩽𝔼[I
a(x) x⩽q
]. On the other hand, the function c → 𝔼[I
c(x)
x⩽q
]. On the other hand, the function c → 𝔼[I
c(x) x⩽q
] is non-decreasing, and
x⩽q
] is non-decreasing, and  x⩽q
]. Then c
1⩽a. We now prove that c
2>a. Actually, over Ω2={x>q}, the indemnity Ĩ* is strictly greater than a. Then Δ2=E[Ĩ*(X)
x⩽q
]. Then c
1⩽a. We now prove that c
2>a. Actually, over Ω2={x>q}, the indemnity Ĩ* is strictly greater than a. Then Δ2=E[Ĩ*(X) x>q
]⩾aα>0. If c
2⩾q then c
2⩾a (because q>a by assumption). If c
2<q, as
x>q
]⩾aα>0. If c
2⩾q then c
2⩾a (because q>a by assumption). If c
2<q, as  hence c
2>a. Thus, c
2>a is proved.
hence c
2>a. Thus, c
2>a is proved.
We continue the proof of Lemma B.1.
As c 1⩽a, Pr{J 1 *(x)>a}=α. Moreover, we have Pr{J 2 *(x)>a}=α because c 2>a. For i=1, 2, 𝔼[Ĩ *(x)]=𝔼[J i *(x)],0⩽J i *(x)⩽x and Pr{J i *(x)>a}=α. Therefore J i *(x) satisfies the constraints of Problem 4.1. As Ĩ* is an optimal solution of Problem 4.1,

For i = 1, we have

Thus,  Because of the optimality of J
1, and the fact that the solution is unique (a.s.) over Ω1 (by Proposition 2.1),
Because of the optimality of J
1, and the fact that the solution is unique (a.s.) over Ω1 (by Proposition 2.1),

The proof is similar when i = 2. Lemma B.1 is proved. □
The next lemma precisely characterizes the optimal indemnity among the set of double-capped indemnities.
Lemma B.2. Given 0⩽c
1<c′1⩽a<c′2<c
2, define  and
and  then:
then:

Proof. Let  and
and  One has Y
2⩽Y′2⩽Y′1⩽Y
1. Owing to the concavity of V(.), we have
One has Y
2⩽Y′2⩽Y′1⩽Y
1. Owing to the concavity of V(.), we have

Over {x>q}, Y′1=w+P−(1+η)c′1 and Y 1=w+P−(1+η)c 1 are constant.
Thus, we have

By definition, 𝔼[I] = 𝔼[I′]. Then we have

Then by combining the last two formulae we obtain

We now consider the region {c 1⩽x⩽q}. Over this region {c 1⩽x⩽q}, we have

By the concavity of V(.), for each ω∈Ω such that x(ω)∈[c 1,q], we have

Moreover, (B5) holds for ω such that x(ω)⩽c 1 as well, because Y 1(ω) = Y′1(ω) over {x⩽c 1}. Therefore, (B5) holds for all ω such that x(ω)⩽q. Taking expectation over the region {x⩽q}, we obtain a second important inequality:

Therefore, combining the two inequalities in our previous discussion, we obtain

Equivalently,

Thus Lemma B.2 is proved. □
We are now ready to prove Proposition 4.1. Assume Δ min <Δ<Δ max .
Existence of the optimal indemnity
If there exists a non-decreasing solution to Problem 4.1, Lemma B.1 implies that the non-decreasing optimal solution must be a double-capped indemnity. Therefore, it suffices to prove that one double-capped indemnity is an optimal solution. Define a function g(c), for c⩾a by

g(c) is the actuarial value of the double-capped indemnity with the first cap level a, and the second layer cap is c. The function g(c) is increasing and continuous with respect to the argument c. Clearly, g(a) = Δ min , g(N) = Δ max and define Δ med = g(q). Then for any Δ∈(Δ min , Δ max ), there exists a unique c>a such that g(c) = Δ. Moreover, c⩾q if and only if Δ⩾Δ med .
We prove that the double-capped indemnity

is an optimal indemnity of Problem 4.1. For this purpose, let I = I(x) be another indemnity that is non-decreasing and subject to the constraints that 𝔼[I(x)] = Δ, 0⩽I(x)⩽x and Pr{I(x)>a} = α. It suffices to prove that

As I is assumed to be non-decreasing and Pr{I>a} = α, then

Let I
1 = I
 x⩽q
and I
2 = I
x⩽q
and I
2 = I
 x>q
, and define Δ1 and Δ2 by
x>q
, and define Δ1 and Δ2 by

Choose c 1 and c 2 such that

By using Proposition 2.1, one has

Therefore,

where

Over {x⩽q}, I(x)⩽a. Then by the same proof of the Claim in the proof of Lemma B.1, we have c
1⩽a. On the other hand, as  , and c
1⩽a, c
2⩽c. Moreover, c
1<a implies c
2<c, and c
1 = a implies that c
2 = c. By Lemma B.2, and note that c
1⩽a⩽c
2⩽c, we obtain
, and c
1⩽a, c
2⩽c. Moreover, c
1<a implies c
2<c, and c
1 = a implies that c
2 = c. By Lemma B.2, and note that c
1⩽a⩽c
2⩽c, we obtain

Owing to (B7) and (B8), we have proved the existence part.
Uniqueness of the non-decreasing optimal indemnity
Assume that there exists another non-decreasing optimal indemnity for Problem 1. Then by Lemma 4.1, it must be a double-capped indemnity with the first layer cap c 1⩽a and the second layer cap c 2>a. By Lemma B.2, as this indemnity is optimal, c 1=a. Therefore, the uniqueness follows from the strictly increasing property of the function g(c). Proposition 4.1 is proved.
Appendix C
Proof of Proposition 1: Optimal design for the insured
We start with an extension of Proposition 2.1 [2] with further constraints on the indemnity I(x).
Lemma C.1. Let A be a measurable subset of Ω with positive measure Pr{A}, and fixed positive numbers P, a and Δ. Assume that Δ<𝔼[x
 A
].
A
].
-
1
If Δ⩽𝔼[min{x,a}
 A
], then there exists d>0 such that min{I
d
(x),a}
A
], then there exists d>0 such that min{I
d
(x),a} A
solves the optimal solution of the following problem:
A
solves the optimal solution of the following problem: 
where d is determined by 𝔼[min{I d (x),a}
 A
] = Δ. Moreover, min{I
d
(x),a }
A
] = Δ. Moreover, min{I
d
(x),a }  A
is the unique optimal indemnity subject to the corresponding constraints (a.s.).
A
is the unique optimal indemnity subject to the corresponding constraints (a.s.). -
2
If 𝔼[a
 A
]⩽Δ⩽E[max{x,a}
A
]⩽Δ⩽E[max{x,a} A
], then there exists d>0 such that max{I
d
(x),a}
A
], then there exists d>0 such that max{I
d
(x),a} A
solves the optimal solution of the following problem:
A
solves the optimal solution of the following problem: 
where d is determined by 𝔼[max{I d (x),a}
 A
] . Moreover, max{I
d
(x),a}
A
] . Moreover, max{I
d
(x),a} A
is the unique optimal indemnity subject to the corresponding constraints (a.s.).
A
is the unique optimal indemnity subject to the corresponding constraints (a.s.).
Proof. For A = Ω, a similar result has been presented in Cummins and Mahul (2004) for an upper limit on coverage under an actuarial value constraint E[I(x)] = Δ. It can also be proved similarly as Proposition 2.1. Hereafter, we provide the proof when Pr{A} = 1. In the general case the proof is the same by adding  A
throughout the discussion. The proof of the second part is similar and is hence omitted.
A
throughout the discussion. The proof of the second part is similar and is hence omitted.
Given λ > 0, consider the following optimization problem:

for a parameter λ⩾U −1(w 0−P). It is easy to verify that min{(x−(w 0−P−[U′]−1(λ))+,a} solves the above optimization problem. As Δ⩽𝔼[min{x,a}], there exists λ *⩾U −1(w 0−P) such that

Thus, a capped deductible min{I d (x),a} with d = w 0−P−[U′]−1(λ*) solves the optimal insurance design problem. The proof is done when Pr{A} = 1.□
Before proving Proposition 5.1, we present two lemmas that characterize the optimal indemnity among a group of non-decreasing indemnities with the form  or
or  respectively.
respectively.
Lemma C.2. Given α>0, q, the (1−α) quantile (which is greater than a by assumption), d 1∈[0, q] and d 2∈[0, q−a]. Denote by I d 1,d 2 the following indemnity:

where d
1 and d
2 satisfy  . There exists a unique d
*∈[0,q−a] such that:
. There exists a unique d
*∈[0,q−a] such that:

Moreover, for all d
1∈[0,q] and d
2∈[0,q−a] such that  we have
we have

Proof. As M(q)=𝔼[(X−(q−a))+] and using the continuity of the distribution of the loss x and thus of the mapping d * → 𝔼[I d*,d*], the existence and the uniqueness of d * are proved.
To prove the second part, it is worth explaining the idea first. We first interpret d
2 as a function of the variable d
1, say d
2 = φ(d
1), if {d
1,d
2} satisfy  One easily obtains
One easily obtains

By construction, for all  Denote by g the density of the loss x and differentiate this equation with respect to d
1. Then
Denote by g the density of the loss x and differentiate this equation with respect to d
1. Then

which is obviously negative. Hence, d 2 = φ(d 1) is a decreasing function of d 1. Let

It is straightforward to obtain

Therefore the function Φ(.) has a unique maximum when d
1 = φ(d
1), that is when d
1 = d
2 = d
*. Indeed, the integral  is always positive; thus Φ′(d
1) is positive over {d
1>d
*} and negative over {d
1>d
*} because U′(.) is decreasing.
is always positive; thus Φ′(d
1) is positive over {d
1>d
*} and negative over {d
1>d
*} because U′(.) is decreasing.
Lemma C.3. Given α>0, q, the (1−α)-quantile (assumed to be greater than a), d
1∈[0, q], d
2>0, f>a. Denote by the following indemnity:
the following indemnity:

where {d
1,d
2,f} satisfy that  . Then:
. Then:

where I d*,d* is defined in lemma C.2.
Proof. The proof of this lemma builds on the same ideas as the proof of Lemma 2. We proceed in two steps.
Step 1: We first assume d
1 is fixed. Then we define (implicitly) d
2 as a function of the floor f by using the equation  . Write d
2 = ψ(f). Differentiating the equality
. Write d
2 = ψ(f). Differentiating the equality  with respect to f, we obtain
with respect to f, we obtain

which proves in particular that ψ(f) is an increasing function of the floor f. Define

After some computations, we have

Over the range x∈(q,f+ψ(f)), −ψ(f)<f−x, thus Ψ′(f)<0. Hence Ψ(f) is decreasing for f>a. Therefore, by Lebesgue dominance theorem, for some d 2,

Hence I
d
1,d
2,f is dominated by the indemnity of the form min{I
d
1, a} x⩽q
+max{I
d
1, a}
x⩽q
+max{I
d
1, a} x>q
.
x>q
.
Step 2: In this step we consider the indemnity of the form (by abuse of the notation)

with the actuarial value Δ. We prove that the expected utility of the indemnity of the form  is dominated by the expected utility of the indemnity with d
2=q−a. If d
2⩽q−a, then I
d
1,d
2 is reduced to the same indemnity I
d
1,d
2 in Lemma C.2. Therefore, in the subsequent proof, we only consider d
2>q−a.
is dominated by the expected utility of the indemnity with d
2=q−a. If d
2⩽q−a, then I
d
1,d
2 is reduced to the same indemnity I
d
1,d
2 in Lemma C.2. Therefore, in the subsequent proof, we only consider d
2>q−a.
We now express d
1 as a function of d
2, say χ(d
2). Write  . Since Δ>M(q), then χ(d
2)≤q−a. Moreover,
. Since Δ>M(q), then χ(d
2)≤q−a. Moreover,

Define  , by straightforward computation we have
, by straightforward computation we have

As d 1=x(d 2)⩽d 2, then x′(d 2)<0. Therefore x(d 2)⩽x(q−a) for all d 2>q−a. Then the lemma follows from Lemma C.2 easily.□
Proof of Proposition 1. Assume  (q)<Δ<Δ
max
.
(q)<Δ<Δ
max
.
Step 1. We verify the revelation principle in this step, that is, if there exists an optimal solution I * to Problem 5.1, then there exists a non-decreasing optimal indemnity I * to Problem 5.1. Indeed, if I is an optimal solution then its non-decreasing rearrangement is also an optimal solution. Constraints are satisfied by Ĩ because of the properties of the non-decreasing rearrangement. Moreover, by Hardy–Littlewood inequality (B2) with L(x, t)=U(w 0−P−x+t), one has

because x → U′(w 0−P−x+t) is increasing.
Step 2. Assume that I * is one non-decreasing optimal indemnity of Problem 5.1. As I * is non-decreasing, and Pr{I *>a} = α, then we have

Let I
1
*(x) = I
*(x) x⩽q
,I
2
*(x) = I
*(x)
x⩽q
,I
2
*(x) = I
*(x) x>q
, and Δ
I
= 𝔼[I
i
*(x)] for i=1, 2.
x>q
, and Δ
I
= 𝔼[I
i
*(x)] for i=1, 2.
We first deal with I 1 *(x). Clearly, Δ1⩽𝔼[min{x,a}1 x⩽q ]. It is also easy to see that I 1 *(x) solves the following optimal problem

subject to constraints 0⩽J(x) x⩽q
⩽x
x⩽q
⩽x
 x⩽q
, J(x)
x⩽q
, J(x) x⩽q
⩽a and 𝔼[J(x)
x⩽q
⩽a and 𝔼[J(x) x⩽q
] = Δ1. Then by Lemma C.1, there exists d
1>0 such that
x⩽q
] = Δ1. Then by Lemma C.1, there exists d
1>0 such that

Step 3. We characterize I
2
*
 x>q
in this step. Define
x>q
in this step. Define

Then  n
⊆
n
⊆ n+1 and ⋃
n
n+1 and ⋃
n
 n
= {I(x)>a} = {x>q}. For n>>0 (which means that there exists p⩾0 such that for all n⩾p), by Lemma C.1, there exists d
n
⩾0 such that
n
= {I(x)>a} = {x>q}. For n>>0 (which means that there exists p⩾0 such that for all n⩾p), by Lemma C.1, there exists d
n
⩾0 such that

We consider the two cases separately.
Case 1. If for all n>0,  then
then  . Therefore d
n
= d
n+1 as long as Pr{
. Therefore d
n
= d
n+1 as long as Pr{ n
}>0. Hence there exists d⩾0 such that d
n
= d,n>0. So I
2
*
n
}>0. Hence there exists d⩾0 such that d
n
= d,n>0. So I
2
*
 x>q
= (x−d)+
x>q
= (x−d)+
 x>q
.
x>q
.
Case 2 If there exists n such that Pr{I
n
≠(x−d
n
)+: n
}>0, then Pr{I
n
= a+1/n:A
n
}>0. Consider
n
}>0, then Pr{I
n
= a+1/n:A
n
}>0. Consider  over
over  n+1. As I
n+1 is non-decreasing, then Pr{I
n+1=a+1/(n+1):
n+1. As I
n+1 is non-decreasing, then Pr{I
n+1=a+1/(n+1): n+1} = 0. Otherwise, I
n+1 would start from a line a+1/(n+1), and has another line in the middle a+1/n, which is impossible for a floored deductible indemnity (because of (C10) and of
n+1} = 0. Otherwise, I
n+1 would start from a line a+1/(n+1), and has another line in the middle a+1/n, which is impossible for a floored deductible indemnity (because of (C10) and of  n
⊆
n
⊆ n+1). Therefore, I
n+1=max{a+1/n,(x−d
n
)+}. Continuing this procedure we have
n+1). Therefore, I
n+1=max{a+1/n,(x−d
n
)+}. Continuing this procedure we have

Hence we see that, there exists n such that

By combining Steps 2 and 3 together, we have either I
* = min{a,(x−d
1)+} x⩽q
+max{f,(x−d
2)+}
x⩽q
+max{f,(x−d
2)+} x>q
,f>a or I
* = min{a,(x−d
1)+}1
x⩽q
+(x−d
2)+
x>q
,f>a or I
* = min{a,(x−d
1)+}1
x⩽q
+(x−d
2)+
 x>q
. Then by using Lemmas C.2 and C.3 together, the optimal indemnity is given by
x>q
. Then by using Lemmas C.2 and C.3 together, the optimal indemnity is given by

where d * is defined in Lemma C.2. Then we find out one non-decreasing optimal indemnity based on this characterization. The uniqueness follows from the proof procedure.
The proof of Proposition 5.1 is then completed. □
Rights and permissions
About this article
Cite this article
Bernard, C., Tian, W. Insurance Market Effects of Risk Management Metrics. Geneva Risk Insur Rev 35, 47–80 (2010). https://doi.org/10.1057/grir.2009.2
Published:
Issue Date:
DOI: https://doi.org/10.1057/grir.2009.2


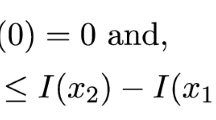





 x⩽q
+I
c(x)
x⩽q
+I
c(x) x>q
is the optimal indemnity of Problem 4.1. Moreover, the non-decreasing optimal indemnity of Problem 4.1 is unique a.s. If Δ=Δ
max
, this is in fact J
a,q
(x).
x>q
is the optimal indemnity of Problem 4.1. Moreover, the non-decreasing optimal indemnity of Problem 4.1 is unique a.s. If Δ=Δ
max
, this is in fact J
a,q
(x).

 (q), then there exists a positive d⩾q−a such that the deductible indemnity I
d
(x) is the optimal indemnity of Problem 2.2. The Var constraint is redundant.
(q), then there exists a positive d⩾q−a such that the deductible indemnity I
d
(x) is the optimal indemnity of Problem 2.2. The Var constraint is redundant. (q)<Δ⩽Δ
max
, then the unique non-decreasing optimal indemnity I
* of Problem 5.1 is written as
(q)<Δ⩽Δ
max
, then the unique non-decreasing optimal indemnity I
* of Problem 5.1 is written as 

 x
⩽
q
as shown in
x
⩽
q
as shown in 

 A
], then there exists d>0 such that min{I
d
(x),a}
A
], then there exists d>0 such that min{I
d
(x),a} A
solves the optimal solution of the following problem:
A
solves the optimal solution of the following problem: 
 A
] = Δ. Moreover, min{I
d
(x),a }
A
] = Δ. Moreover, min{I
d
(x),a }  A
is the unique optimal indemnity subject to the corresponding constraints (a.s.).
A
is the unique optimal indemnity subject to the corresponding constraints (a.s.). A
]⩽Δ⩽E[max{x,a}
A
]⩽Δ⩽E[max{x,a} A
], then there exists d>0 such that max{I
d
(x),a}
A
], then there exists d>0 such that max{I
d
(x),a} A
solves the optimal solution of the following problem:
A
solves the optimal solution of the following problem: 
 A
] . Moreover, max{I
d
(x),a}
A
] . Moreover, max{I
d
(x),a} A
is the unique optimal indemnity subject to the corresponding constraints (a.s.).
A
is the unique optimal indemnity subject to the corresponding constraints (a.s.).