Risk-sharing Contracts with Asymmetric Information

Abstract

We examine how risk-sharing is impacted by asymmetric information on the probability distribution of wealth. We define the optimal incentive compatible agreements in a two-agent model with two levels of wealth. When there is complete information on the probability of the different outcomes, the resulting allocation satisfies the mutuality principle (which states that everyone's final wealth depends only upon the aggregate wealth of the economy). This is no longer true when agents have private information regarding their probability distribution of wealth. Asymmetry of information (i) makes ex-post equal sharing unsustainable between two low-risk agents, and (ii) induces exchanges when agents have the same realization of wealth.

Introduction

Transactions over the counter (OTC) are commonly used among financial institutions as a complement to the market. For instance, debt owners can use OTC contracts to transfer default risk to other financial organizations. Such contracts are also used by insurance companies when they group together for reinsurance purposes. These pools of insurance companies are designed to share risk and avoid recourse to a reinsurance company, under what amounts to a “mutual risk-sharing agreement”. At the opposite end of the financial world, mutual agreements in small communities or villages are other examples of such risk-sharing mechanisms. The purpose of these agreements is essentially to mitigate risk for both parties through mutual diversification.

When individual probability distributions of wealth are identically distributed (but not necessarily independent) the optimal agreement is obviously always to equally divide the total wealth. By aggregating and dividing identically distributed risks, these contracts indeed minimize risk in the sense of the mean-preserving spread criterion.¹

In this paper, we introduce heterogeneity (individual risks are not identically distributed) and asymmetry of information (individuals don’t know their partner's risk). The question adressed here is to investigate the optimal risk-sharing contracts with such features. Indeed, when individual probability distributions of wealth are not identically distributed, a simple equal sharing of the total bundle can be unacceptable for “low-risk” individuals. When, moreover, these distributions are private information, a low-risk party can be reluctant to share risk, fearing that the other may be highly exposed. In these cases, equal sharing must be replaced by more sophisticated contracts. We precisely study this problem in this paper and analyse the consequences of hereterogeneity on the one hand and asymmetry of information on the other. In particular, we derive the main properties of optimal contracts and investigate their efficiency properties.

As far as efficiency is concerned, one of the main results of general equilibrium theory extended to uncertainty is the mutuality principle (see, for instance, Gollier (2001) or the seminal paper by Borch (1962)). Under complete information, all Pareto efficient allocations of risk are such that the final wealth of each agent only depends on the final value of aggregate wealth.² The allocation of this aggregate wealth then depends on the risk aversion of the agents. One of the questions addressed here is whether this principle can be maintained in an incomplete information framework.

We consider the case of two risk-averse agents and two levels of (random) individual wealth. Either the agent suffers damage or not. We allow agents to be heterogeneous regarding their probability distribution of wealth: the individual probability of suffering damage can either be low or high. As our intention is to focus on risk heterogeneity, we assume that agents are identical regarding their risk aversion. To share risk, the agents are willing to sign a bilateral contract that specifies contingent payments. To model this bargaining, we introduce a third uninformed party who plays the role of the principal in a “principal–two agents” relationship. This principal designs a risk-sharing mechanism which allocates wealth, in each state of nature, according to the self-declared risk types of the agents. We look for mechanisms that are Bayesian incentive, that is, such that telling the truth is a Bayesian Nash equilibrium. Finally, we focus on mechanisms that maximize the ex-ante utilitarian criterion.

The main findings of this paper are the following:

First of all, under complete information, equal sharing is obviously optimal when the agents are identical. It remains optimal when they are different provided the heterogeneity of risks is not too high and risk aversion not too low. Anyway, under complete information, and for all levels of risk, the optimal sharing rule always satisfies the mutuality principle.

Under asymmetric information, equal sharing is optimal for a larger range of risk heterogeneity.³ However, when heterogeneity is too high or risk aversion too low, the introduction of asymmetric information rules out the mutuality principle. More surprisingly, the optimal rule provides an unequal sharing of the total wealth when both agents declare to be low risk, and induces transfers even in states of nature where agents have the same realization of wealth. Compared to the case of complete information, it also induces changes in the direction of transfer (from low-risk to high risk) in some states of nature for most utility functions of the Harmonic Absolute Risk Aversion (HARA) class. Finally, when the asymmetry of information leads to a loss of efficiency, this loss is entirely borne by low-risk agents, as in the case of insurance companies (see Rothschild and Stiglitz, 1976; Chade and Schlee, 2008).

We now discuss the relationship of this paper with the literature. First, our work fits into the literature on asymmetric information in risk-sharing agreements. Previous literature mainly focus on moral hazard (Doepke and Townsend, 2006) or inequality in wealth (Genicot, 2006). Few papers analyse heterogeneity in the wealth distribution and then merely focus on equal sharing of wealth (Ligon and Thistle, 2005). We contribute to this literature by analyzing the optimal sharing rule between agents that differ in their probability distribution of wealth.

Risk heterogeneity is taken into consideration to a greater extent in the literature on micro-credit (see, for example, Townsend (2003) on moral hazard or Armendariz and Gollier (2000) on adverse selection). In this literature, however, the interest rate is the same for every type of individual and the bank is unable to extract information about the risk level of the borrowers. Here, we model a situation where the principal wants to extract information about the wealth distribution of each agent and provides the optimal risk-sharing agreement.

Our work also fits into the literature on informal insurance, and more precisely on the rejection of the mutuality principle in informal insurance (see Townsend, 1994). Previous works mostly explain this limitation by limited commitment and assume identical agents (see Kimball, 1988; Coate and Ravallion, 1993; Kocherlakota, 1996; Ligon et al., 2002; and Genicot and Ray, 2003, among others). In this paper, we suggest asymmetric information on wealth distribution as an alternative explanation.

Our model can moreover be seen as contributing to the study of reinsurance markets. In his seminal paper, Borch (1960) models reciprocal reinsurance treaties as a two-person cooperative agreement similar to ours. Doherty (1997) adds moral hazard to the discussion. Our paper contributes to the reinsurance theory literature by focusing on adverse selection.

Our work is also related to the literature on adverse selection in insurance companies. Following Rothschild and Stiglitz (1976), many authors have analysed how insurance companies deal with asymmetric information on the distribution of wealth. As we focus on a principal–agents model, our paper is more closely linked with works on monopoly insurance (see, for example, Stiglitz, 1977; Landsberger and Meilijson, 1994; Chade and Schlee, 2008). The main result of these papers is to show that the optimal contract amounts to providing the “high type” (high-risk-type or the most risk-averse agents) with full insurance and the other type(s) with only partial insurance. Under general equilibrium, authors often use the Rothschild–Stiglitz model to discuss risk sharing. Following Prescott and Townsend (1984), Bisin and Gottardi (2006) study the efficient equilibria in a competitive economy in the context of Rothschild and Stiglitz (i.e., when agents have private information regarding the probability distribution of their endowment).

Our work, however, differs from the literature on insurance companies through the distinction between private insurance contracts and risk-sharing agreements. Whereas insurance companies can rely on external capital, risk-sharing agreements only rely on the wealth of the contracting parties. This has an important modelling consequence: in our case, the resource feasibility constraint has to be satisfied in every state, whereas in the case of insurance companies it has to be satisfied only in expectation. Put another way, in our paper agents always bear aggregate risk, whereas in the case of private insurance this risk is borne by the risk-neutral insurer(s).

A recent paper by Picard (2009) tries to fill the gap between the studies on insurance companies and on mutual risk-sharing agreements. Our work, however, differs from Picard's in that he studies market equilibrium in a competitive framework whereas we focus on optimal risk sharing in a framework where it is the only instrument available to mitigate risk.

Finally, our work contributes to the literature on contract theory, by introducing behavior toward risk into the mechanism design (as the transfers enter into the utility function). This leads to non-quasi-linear preferences, thereby adding technical issues to those usual in Bayesian implementation, notably type-dependant outside option. This implies, in particular, that the objective function is not supermodular under contracts that satisfy the Bayesian incentive constraints.

The rest of this paper is structured as follows: Section “The model” introduces the two-agent model of risk sharing. Section “The complete information benchmark” discusses the benchmark case of complete information. In Section “Asymmetric information”, we analyse the incomplete information case and characterize the optimal Bayesian incentive compatible sharing rule. Our concluding remarks and suggestions for future research are in Section ‘Conclusion’

The model

Consider two risk averse agents who face a risk on wealth. Wealth can either equal x̄ or x=x̄−d (d>0). Individual realizations are assumed to be independent with θ _i the probability that individual i(i=1, 2) has a bad outcome x̄. θ _i can take two possible values θ and θ̄ with 0<θ<θ̄<1 (Θ≡{θ, θ̄}).⁴ There are hence four states of nature ω: (0, 0), (1, 0), (0, 1) and (1, 1) that arise respectively with probabilities (1−θ ₁)(1−θ ₂), θ ₁(1−θ ₂), (1−θ ₁)θ ₂ and θ ₁ θ ₂. We denote π(θ ₁, θ ₂, ω), θ _i ∈{θ, θ̄} the probability that state ω occurs when individual 1 is of type θ ₁ and individual 2 of type θ ₂. Let X _i (ω) (either equal to x̄ or x) be the realized level of wealth for individual i in the state ω and X(ω)=X ₁(ω)+X ₂(ω) be the aggregate wealth. Risk types are assumed to be independent⁵ and we note μ̄≡μ(θ̄)≡prob(θ _i =θ̄) and μ≡μ(θ)≡prob(θ _i =θ)=1−μ̄.

Agents have a von Neumann utility function⁶ u(.) which is supposed to be twice differentiable and strictly concave.

The timing is as follows:

• At date 1, agents learn their type.

• At date 2, an uninformed principal proposes a risk-sharing mechanism.

Definition 1

• A risk-sharing mechanism x specifies − in each state of nature − how aggregate wealth is shared among participants according to their type.

  

  • At date 3, agents decide to participate.

  • At date 4, risk on wealth is realized and contract enforced.

We aim to model the optimal contract resulting from bargaining between two agents that have the same bargaining power. To do so, we assume that the benevolent principal puts the same weight on the two agents. As he is not informed of the agents’ type, he uses an ex-ante utilitarian criterion to find the optimal sharing mechanism. Owing to the concavity of u this implies that the mechanism is anonymous (x ₁(θ, θ′, (a, b))=x ₂(θ′, θ, (b, a)) ∀a, b∈{0, 1} and θ, θ′∈{θ̄, θ}).

Let us first examine the benchmark case, where there is complete information on the individual probability distributions of wealth.

The complete information benchmark

In the complete information case, the wealth distributions of both agents are common knowledge. Two antagonistic forces are at work. First, the diversification principle encourages risk-sharing. When X ₁(ω) and X ₂(ω) are identically distributed, (X ₁(ω)+X ₂(ω))/2=X(ω)/2 is less risky (in terms of second-order stochastic dominance) than X _i (ω). Sharing aggregate wealth allows risk diversification and hence welfare improvement. However, faced with heterogeneity in wealth distributions, that is if X ₁(ω) and X ₂(ω) are not identically distributed, low-risk individuals may not be willing to share the total bundle. To be individually rational, the sharing scheme must then be distorted in favour of low-risk agents.

The utilitarian optimal contract is hence the solution of:

It is then easy to state the following result.

Proposition 1

• When there is complete information on individual wealth distributions, the optimal contract (x ₁(θ ₁, θ ₂, ω), x ₂(θ ₁, θ ₂, ω)):

  • always satisfies the mutuality principle (the optimal allocation only depends on aggregate wealth: ∀θ _1, θ ₂ ∈{θ, θ̄}, a, b∈{0, 1}, x _i ((θ ₁, θ ₂, (a, b)))=x _i ((θ ₁, θ ₂, (b, a)));

  • amounts to equal sharing of wealth in any configuration, if risk aversion is high and heterogeneity in wealth distributions is low, that is if

    

  • if risk aversion is too low and heterogeneity too high ((u(◯)−u(x)/u(x̄)−u(◯))<((1−θ)θ̄/θ(1−θ̄)))

    • a equal sharing is optimal when both agents have the same type (x ₁(θ, θ, ω)=x ₁(θ̄, θ̄, ω)=x ₂(θ̄, θ̄, ω)=x ₂(θ, θ, ω)=X(ω)/2);

    • b a low-risk agent always gets more than average wealth when paired with a high-risk agent (x ₁(θ, θ̄, ω)⩾x ₂(θ, θ̄, ω)∀ω).

Proof: See Appendix. □

Without participation constraints, the optimal utilitarian allocation would amount to equal sharing of the aggregate wealth: x ₁(θ ₁, θ ₂, ω)=x ₂(θ ₁, θ ₂, ω)=X(ω)/2 ∀ω. The participation constraints may, however, make the optimal sharing rule differ from this allocation. Although high-risk agents are always better off under the equal sharing rule than under autarky, this may not be the case for low-risk individuals. Indeed, a low-risk agent benefits from equal sharing when paired with an individual of the same risk type, but may prefer to remain alone when matched with a high-risk agent.

When Eq. (2) is satisfied, equal sharing is optimal even if individuals do not face the same probability of damage. The left-hand side (greater than 1 for risk-averse agents) is an index of risk aversion whereas the right-hand side (also greater than 1) measures the heterogeneity of wealth distributions. It can indeed be written as 1+((θ̄−θ)/θ(1−θ̄)). The right-hand side of (2) therefore increases with a mean-preserving spread of wealth distributions (θ̄−θ). Equal sharing is thus optimal when heterogeneity is sufficiently low or when risk aversion is sufficiently high.

When the above inequality does not hold, that is when heterogeneity is high, equal sharing is not individually rational for low-risk agents. To be participation proof, the optimal risk-sharing rule must provide the low-risk individual with more than average wealth in every state of nature.

Asymmetric information

We now turn to the incomplete information setting. When agents have private information on their wealth distribution, the risk-sharing agreement must be interpreted as a mechanism. According to the revelation principle, the principal offers a menu of contracts depending on the reported risk types that gives agents the incentive to truthfully report their risk type.

Bayesian incentive compatibility

In our setting, truthful reporting is a Bayesian-Nash equilibrium if, for agent one:

And similarly for agent 2 (labelled BIC₂(θ̄) and BIC₂(θ)).

These interim Bayesian incentive constraints state that, knowing their own risk type but ignoring the type of the other party, all agents are better off (in expectation) truthfully reporting their type. As it only depends on realizations (and not on type), equal sharing obviously satisfies these Bayesian incentive constraints.

Moreover, under incomplete information, participation in the agreement is determined at the interim stage. The participation constraints therefore become for agent one:

And similarly for agent 2 (labelled PC₂(θ̄) and PC₂(θ)).

The next proposition states that equal sharing is optimal if risk aversion is high and expected heterogeneity low.

Proposition 2

• When agents have private information regarding their wealth distribution, equal sharing is optimal if (u(◯)−u(x))/(u(x̄)−u(◯))⩾((1−θ)E(θ))/(θ(1−E(θ))).

Proof: See Appendix. □

Relative to the benchmark case of complete information, equal sharing is therefore more likely to be optimal. Indeed, the threshold (1−θ)E(θ)/θ(1−E(θ)) is lower than that obtained in the complete information setting ((1−θ)θ̄/θ(1−θ̄)). This comes from the simple fact that, for a low-risk individual, there is a chance to face another low-risk individual.

The asymmetry of information therefore has no impact on the optimal sharing rule when risk aversion is high and expected heterogeneity is low. In such cases, risk sharing does not entail any loss of efficiency due to asymmetric information.

Violation of the mutuality principle

When expected heterogeneity is great, that is when ((u(◯)−u(x))/(u(x̄)−u(◯))<((1−θ)E(θ))/(θ(1−E(θ)))), the participation constraint of low-risk agents binds at the optimum. Suppose first that incentive constraints do not matter. It is easy to see that the optimal sharing rule under participation constraints alone would specify x ₁(θ, θ̄, ω)⩾X(ω)/2⩾x ₁(θ̄, θ, ω) and x ₁(θ̄, θ̄, ω)=x ₁(θ, θ, ω)=X(ω)/2 ∀ω. This would give high-risk individual a strong incentive to cheat on her type. She would thus be better off declaring herself θ whatever the type her opponent claimed to be (x ₁(θ, θ̄, ω)⩾x ₁(θ̄, θ̄, ω) and x ₁(θ, θ, ω)⩾x ₁(θ̄, θ, ω)). Therefore, the optimal allocation under complete information does not satisfy the Bayesian incentive constraints of high-risk individual (BIC _i (θ̄)). It follows that, when the participation constraint of low-risk agent binds, the incentive constraint of high-risk agent necessarily binds too. However, the specificities of our model don’t allow us to rely on usual tools to show that this is the only incentive constraint to bind at the optimum. We discuss more deeply this issue in Section ‘The case of HARA preferences’. Before turning to this discussion, we focus in the present section on general results that can be obtained from the fact that when heterogeneity is great, the incentive constraints of high-risk individual necessarily binds.

The general program under incomplete information writes:

The solution is characterized in the following proposition.

Proposition 3

• When agents have private information regarding their wealth distribution and heterogeneity is high ((u(◯)−u(x))/(u(x̄)−u(◯)))<(((1−θ)E(θ))/(θ(1−E(θ)))).

  • 1 The mutuality principle is not sustainable: agents bear residual individual risk in some configurations.

  • 2 The optimal agreement implies some exchanges when agents have the same realization of wealth.

Proof: See Appendix. □

First of all, it is worth noting that autarky is never optimal (see proof in appendix) and that the program has a unique solution. As shown above, in specifying equal sharing when both agents declare the same risk type, and giving more than half the aggregate wealth to the low-risk agent when individuals are of different types, the complete information rule violates the Bayesian incentive constraint for high-risk agents. To prevent these agents from cheating on their type, the principal has to distort the equal sharing contract when both agents claim to be low risk. By giving less to the agent that suffers the damage in these cases (x ₁(θ, θ, (0, 1))>◯>x ₁(θ, θ, (1, 0))), the contract makes it less profitable for high-risk individuals to declare themselves θ. Since the optimal allocation depends on individual realizations, the mutuality principle no longer holds. Notice that this result is consistent with empirical studies on risk sharing in developing countries (starting with the seminal paper of Townsend (1994) and followed by Coate and Ravallion, 1993; Kocherlakota, 1996; Ligon et al., 2002; Dubois et al., 2008) as discussed in the introduction.

The above distortion moreover implies that equal sharing cannot be optimal, even when both individuals are low risk. When expected risk heterogeneity is high, the asymmetry of information induces a loss of efficiency by reducing insurance when both agents are low risk. In this sense, asymmetric information here has the same impact on risk-sharing, as it has on insurance companies (see Rothschild and Stiglitz, 1976; Chade and Schlee, 2008): a reduction in the coverage offered to low-risk agents.

For the agreement to remain attractive to low-risk agents, however, it has to compensate for previous distortions. This is done partly by specifying transfers from the high-risk to the low-risk individual when neither of the two agents suffers damage. Therefore, the optimal agreement implies some exchanges when agents have the same realization of wealth.

The case of HARA preferences

To describe more precisely the optimal agreement under asymmetric information, we need to establish which constraints bind at the optimum.

The particular nature of our problem means that this cannot be done with the usual tools. More specifically, we are unable to establish the single-crossing property for the Bayesian incentive constraints. Many characteristics make our model non-standard, preventing us from using this standard simplifying property. In the case of risk-sharing (contrary to the usual principal-agent models), transfers enter into the utility function. This makes preferences non-quasi-linear and the objective function not supermodular. Consequently, ex-post (that is, after transfer) utility is not increasing with type. Moreover, the outside option is here type-dependent, so the single-crossing property cannot be established in the usual way.

In addition, we cannot rely on lotteries, as Landsberger and Meilijson (1994) do. In their paper on optimal insurance under asymmetric risk aversion, they use randomization of contracts to prove that only one incentive constraint binds at the optimum. Arnott and Stiglitz (1988), however, show that randomization is never desirable when asymmetric information concerns risk type (and not risk aversion). In our case, the use of lotteries cannot weaken the incentive constraints as agents have the same behavior toward risk. Moreover, as the resource feasibility constraint here has to be satisfied in each state, the randomization cannot concern only one type of agent, as in Landsberger and Meilijson.

We are, however, able to solve the problem if agents’ preferences exhibit HARA, that is if u(c)=ξ[η+(c/γ)]^1−γ (note that u(c) is defined ∀c such that η+(z/γ)>0, increasing and concave for ξ(1−γ)γ ⁻¹>0). This broad class of utility functions, labelled Hyperbolic Absolute Risk Aversion by Merton (1971) and Harmonic Absolute Risk Aversion by Gollier (2001), contains Constant Relative Risk Aversion (η=0), Constant Absolute Risk Aversion (γ → +∞) and logarithmic (γ → 1) preferences as special cases.

Proposition 4

• Suppose that agents’ preferences exhibit HARA with γ⩾1/2. Then, when equal sharing is not achievable, the optimal sharing rule under asymmetric information is fully described by:

  

  which implies ∀a∈{0, 1}, θ∈{θ, θ̄}

  

Therefore, the asymmetry of information on the probability distribution of wealth leads to a “counter-intuitive” change in the sign of transfer (from low risk to high risk) in the state (1, 1) when agents declare themselves as different types (x ₁(θ̄, θ, (1, 1))>x).

Proof: See Appendix. □

Whatever the utility function, it can first be proven (all proofs are in the Appendix) by contradiction that the participation constraint of low risks and the incentive constraint of high risks necessarily bind at the optimum, whereas the participation constraint of high risks never binds. However, as stated previously, we cannot use the usual tools to show that only the incentive constraint of low risks does not bind.

To overcome this difficulty, we first derive the optimal allocation assuming that only the incentive constraint of high risks binds. We are then able to prove under HARA preferences with γ⩾(1/2) that the two incentive constraints only cross once in the plane (ν ₁, ν ₂) that fully describes the allocation. It follows that the incentive constraint of low-risk individuals is lax at the optimum. The assumption γ⩾(1/2) does not seem too restrictive. It is always verified for CARA and logarithmic preferences. Moreover, in the case of CRRA utility function, the literature seems to agree on a parameter of relative risk aversion γ larger than one (see Gollier, 2001; Meyer and Meyer, 2005).

Under such a specification, Proposition 4 states that equal sharing is achievable (and thus optimal) when both agents declare themselves high risk (x ₁(θ̄, θ̄, ω)=X(ω)/2 ∀ω). In contrast to low-risk agents, high-risk individuals therefore obtain their first best contract even when there is asymmetric information.

When both agents are low risks, anonymity implies no transfer when realizations of wealth are the same (x ₁(θ, θ, (0, 0))=x̄ and x ₁(θ, θ, (1, 1))=x). However, as shown in Proposition 3, equal sharing has to be distorted when two agents that declared themselves low risk experience different realizations (x ₁(θ, θ, (0, 1))>◯>x ₁(θ, θ, (1, 0))).

Proposition 4, however, states that this mechanism is not sufficient to prevent high risks from cheating. In the complete information setting, it has been shown that a low-risk agent optimally gets more than equal sharing in any state of nature when matched with a high risk (x ₁(θ, θ̄, ω)⩾X(ω)/2 ∀ω). In spite of the above distortion, this still gives high-risk individuals an incentive to cheat. Mechanisms on x _i (θ, θ, ω) indeed reduce the incentive to cheat when a high-risk individual is paired with a low-risk agent. However, the optimal allocation under complete information also gives an incentive to cheat in the case of two high-risk agents as it specifies x ₁(θ, θ̄, ω)⩾X(ω)/2=x ₁(θ̄, θ̄, ω). To be incentive compatible, the optimal contract must therefore provide high-risk agents with more than half the aggregate wealth in some states when agents declare different risk types. To induce the participation of low-risk agents, this has to be done in states relatively less likely for them, that is when the low-risk agent suffers the damage: (θ̄, θ, (0, 1)) and (θ̄, θ, (1, 1)). A low-risk individual would still accept the agreement as the contract would still be welfare improving if she is paired with another low-risk agent. An interesting implication of this result is that asymmetric information entails, in state (1, 1), a change in the sign of transfer (relative to the complete information benchmark). Whereas in this state, the transfer of wealth goes from high risk to low risk when the distributions of wealth are common knowledge, the optimal agreement under asymmetric information specifies a transfer from low to high risk.

The effect on efficiency of asymmetric information thus largely depends on the degree of heterogeneity. When the difference between the probabilities of damage of the two types is weak, there is no loss of efficiency due to the asymmetry of information. To this extent, risk sharing seems more efficient than private insurance under asymmetric information conditions. However, when heterogeneity is high, the asymmetry of information leads to a loss of efficiency with risk-sharing agreements too. As with insurance companies, this loss is entirely borne by low-risk agents. However, it is difficult to compare the mechanisms behind loss of efficiency due to asymmetry of information in the two cases. This is because the optimal risk-sharing agreement depends on the risk types and realizations of both agents, whereas under private insurance the optimal allocations (e.g. Rothschild and Stiglitz, 1976; Bisin and Gottardi, 2006; Chade and Schlee, 2008) only depend on the risk type of the contracting agent.

Conclusion

Our paper contributes to the literature on risk sharing and on mechanism design by characterizing the optimal mutual risk-sharing agreement between two heterogeneous agents in the presence of asymmetric information.

First, by placing the notion of risk within contracts, this work examines non-quasi-linear preferences in Bayesian implementation. In spite of the technical issues this implies (mainly the non-supermodularity of the objective function), we are able to solve the problem for a broad class of HARA utility functions.

Moreover, our paper provides an additional explanation for the failure of the mutuality principle in risk-sharing agreements: asymmetric information on the probability distribution of wealth. When there is complete information on (heterogeneous) wealth distributions, the mutuality principle holds, as the allocation only depends upon the state of nature insofar as it concerns the aggregate realization. However, when agents have private information on their probability distribution of wealth, the optimal risk-sharing agreement does not prevent them bearing residual individual risk. Another striking result of this work is that in order to give agents the incentive to reveal their risk type, a risk-sharing agreement has to specify transfers in some states where agents have the same realization of wealth. Finally, we show that the asymmetry of information induces changes in the sign of transfer in some states of nature (relative to the complete information benchmark) for most utility functions of the HARA class.

By analyzing the effect of asymmetric information on the efficiency of mutual risk-sharing agreements, this work also contributes to the literature on the differences in organizational structure in insurance. We show that the mutual structure copes better with asymmetric information since the asymmetry of information does not necessarily here lead to a loss of efficiency. Moreover, when the asymmetry of information leads to a loss of efficiency, the loss is entirely borne by low-risk-type agents, as in the case of insurance companies (Rothschild and Stiglitz, 1976; Chade and Schlee, 2008).

In addition to these positive results, our work offers a framework for the design of risk-sharing contracts between financial institutions or insurance companies. In particular, it can be used to precisely design the direction of conditional financial cash flows.

Part of our work seems to be generalizable to situations with more than two agents and/or more than two realizations. First, the condition on the sustainability of equal sharing should be easily extendable to a continuum of agents or realizations. When this first best is not achievable, the failure of the mutuality principle also seems generalizable. To prevent high-risk individuals from cheating about their type, it appears necessary to lower insurance for low-risk agents. This would necessarily be done at the expense of complete risk pooling. A generalization to a continuum of agents would, however, be difficult to model as a contract would then specify an allocation of the aggregate wealth for every possible configuration of individual realization of wealth. Our model can also be extended to correlated wealth distributions. An attempt to study such cases is presented in the working paper version of the present work (Bourlès and Henriet, 2008). Most of our findings (mainly Propositions 1–3) also hold in the case of correlated types, but more attention needs to be given to the issue of single-crossing of incentive constraints.

It is left for future research to use our findings in an empirical context. It would be especially interesting to examine to what extent asymmetric information can explain the failure of the mutuality principle in risk-sharing networks. One test would consists in analyzing whether transfers take place when agents experienced the same realization. If so, this would argue for risk heterogeneity as shown in Proposition 1. Moreover, if the sign of the transfer changes according to whether both agents experience good or bad realizations, this would argue – according to Proposition 4 – for the asymmetric information explanation. Our work also seems to have implications for micro-credits. It would therefore be interesting to extend it to a situation where a bank tries – by setting the interest rate – to extract information about whether each of two borrowers involved in a micro-credit agreement is investing in a safe or a risky project.

Appendix

Proof of Proposition 1

If the Participation Constraints do not bind at the optimum, the solution of the utilitarian program is obviously: x ₁(θ ₁, θ ₂, ω)=x ₂(θ ₁, θ ₂, ω)=X(ω)/2. This solution satisfies the participation constraints if (1−θ ₁)θ ₂(u(◯)−u(x̄))+(1−θ ₂)θ ₁(u(◯)−u(x))⩾0 That is: ((u(◯)−u(x))/(u(x̄)−u(◯)))⩾((1−θ ₂)θ ₁/(1−θ ₁)θ ₂). Therefore, as soon as ((u(◯)−u(x))/(u(x̄)−u(◯)))⩾((1−θ)θ̄/(1−θ̄)θ), – which is the biggest possible value of (1−θ ₂)θ ₁/(1−θ ₁)θ ₂ – part (ii) of Proposition 1 is proven.

As (u(◯)−u(x))/(u(x̄)−u(◯))⩾1, participation constraints can bind only when θ ₁≠θ ₂. The general program is:

Let π(θ, θ̄, ω), α(ω), γ ₁, γ ₂ be the Lagrange multipliers of this program and h=u′⁻¹. We have:

Using x ₁(θ, θ̄, ω)+x ₂(θ, θ̄, ω)=X(ω) allows to conclude that X(ω)=X(ω′) → α(ω)=α(ω′) → x _i (θ, θ̄, ω)=x _i (θ, θ̄, ω′) that is the mutuality principle (i). Moreover, we have, using (A.2), ∀ω either x ₁(θ, θ̄, ω)⩾x ₂(θ, θ̄, ω) or x ₁(θ, θ̄, ω)⩽x ₂(θ, θ̄, ω). It is easy to see that assuming x ₁(θ, θ̄, ω)⩽x ₂(θ, θ̄, ω)∀ω implies x ₁(θ, θ̄, ω)=x ₂(θ, θ̄, ω). Indeed as ∑_Ω π(θ, θ̄, ω)u(X ₁(ω))>∑_Ω π(θ, θ̄, ω)u(X ₂(ω)), x ₁(θ, θ̄, ω)⩽x ₂ (θ, θ̄, ω) implies ∑_Ω π(θ, θ̄, ω)[u(x ₂ (θ, θ̄, ω))−u(X ₂(ω))]>∑_Ω π(θ, θ̄, ω)[u(x ₁(θ, θ̄, ω))−u(X ₁(ω))]⩾0, that is γ ₂=0⩽γ ₁. Then, as h is decreasing x ₁(θ, θ̄, ω)⩾x ₂(θ, θ̄, ω). Hence (iii) is proven. □

Proof of Proposition 2

If the Bayesian Participation Constraints do not bind at the optimum, the solution of the utilitarian program is obviously: x ₁(θ ₁, θ ₂, ω)=x ₂(θ ₁, θ ₂, ω)=X(ω)/2. This satisfies participation constraints if and only if ∀θ ₁, that is if ((u(◯)−u(x))/(u(x̄)−u(◯)))⩾((1−θ ₁)E(θ)/θ ₁(1−E(θ)). Now, as ((1−θ̄)E(θ))/(θ̄(1−E(θ)))⩽1⩽((1−θ)E(θ))/(θ(1−E(θ))), the interim participation constraint is always verified for θ ₁=θ̄ as (u(◯)−u(x))/(u(x̄)−u(◯))⩾1. For θ ₁=θ, the equal sharing rule satisfies the interim participation constraint if: (u(◯)−u(x))/(u(x̄)−u(◯))⩾((1−θ)E(θ))/(θ(1−E(θ))). □

Proof of Proposition 3

Under asymmetric information the program is:

Let α(θ ₁, θ ₂, ω), γ _i (θ), λ _i (θ), be the respective Lagrange multipliers.

As individuals are assumed to be ex-ante identical, x ₁(θ ₁, θ ₂, (a, b))=x ₂(θ ₂, θ ₁, (b, a))=X((b, a))−x ₁(θ ₂, θ ₁, (b, a)) ∀a, b∈{0, 1} and thus α(θ̄, θ, (a, b))=α(θ, θ̄, (b, a)), α(θ̄, θ̄, (1, 0))=α(θ̄, θ̄, (0, 1)), α(θ̄, θ̄, (1, 0))=α(θ, θ, (0, 1)), γ ₁(θ̄)=γ ₂(θ̄)≡ $\overline{γ}$, λ ₁(θ̄)=λ ₂(θ̄)≡ $\overline{λ}$ , γ ₁(θ)=γ ₂(θ)≡γ, λ ₁(θ)=λ ₂(θ)≡λ. □

Lemma 1

• The optimum is unique

Proof of Lemma 1

Let h ₁(θ ₁, θ ₂, ω)≡u(x ₁(θ ₁, θ ₂, ω)), h ₂(θ ₁, θ ₂, ω)≡u(x ₂(θ ₁, θ ₂, ω)) and

In h ₁(.) and h ₂(.) we then have one strictly convex equality constraint and multiple linear inequality constraints. This defines a strictly convex constraint set. Since the gradient of the linear objective is not equal to the gradient of any linear constraint, the optimum must be unique. □

Lemma 2

• The mutuality principle is not sustainable and the optimal sharing rule implies exchange in some states where realizations of wealth are identical. Therefore, autarky is never optimal.

Proof of Lemma 2

The first-order conditions of (A.3) can then be written as:

First of all, when both individuals declare themselves to be the same risk type and have the same initial wealth, anonymity implies: x ₁(θ, θ, (0, 0))=x ₂(θ, θ, (0, 0))=x̄ and x ₁ (θ, θ, (1, 1))=x ₂ (θ, θ, (1, 1))=x, ∀θ∈{θ, θ̄}, (note that this is fortunately confirmed by the first-order conditions).

Now, when agents declare themselves to be the same risk type but have different initial wealth, the first-order conditions lead to:

As θ<θ̄, we have A⩾B and D⩾C. The optimal sharing rule has thus to satisfy:

The Lagrange multiplier in brackets is the one that have to be null in order for the corresponding equation to be satisfied with equality.

The mutuality principle would imply in this setting that x ₁(θ ₁, θ ₂, (0, 1))=x ₁(θ ₁, θ ₂, (1, 0)) and notably that:

• for θ ₁=θ ₂=θ̄, x ₁(θ̄, θ̄, (1, 0))=x ₁(θ̄, θ̄, (0, 1))=x ₂(θ̄, θ̄, (0, 1)) which would lead to λ=0 by (A.4);

• for θ ₁=θ ₂=θ, x ₁(θ, θ, (1, 0))=x ₁(θ, θ, (0, 1))=x ₂(θ, θ, (0, 1)) which would lead to θ̄ $\overline{λ}$ =0 by (A.5).

The mutuality principle would then be sustainable only if the complete information allocation were incentive compatible for both types of individuals (λ= $\overline{λ}$ =0). Thus, the mutuality principle is not sustainable when ((u(◯)−u(x))/(u(x̄)−u(◯)))⩾(((1−θ)E(θ))/(θ(1−E(θ)))).

Finally, when agents declare themselves to be different risk types, the solution can be written as:

As B⩽A, D⩽C the following inequalities hold:

If there were no exchange when realizations of wealth are identical, that is if x ₁(θ̄, θ, (0, 0))=x ₂(θ̄, θ, (0, 0))=x̄ and x ₁(θ̄, θ, (1, 1))=x ₂(θ̄, θ, (1, 1))=x, the six previous ratios would be equal to one. This implies λ= $\overline{λ}$ =0, which has been shown to be impossible when heterogeneity is high. This implies in particular that autarky is not optimal and that the optimal sharing rule calls for exchange in some states where realizations of wealth are identical. □

Proof of Proposition 4

Lemma 3

• The participation constraint for low-risk individuals necessarily binds whereas the participation constraint for high-risk individuals is always strictly satisfied at the optimum.

Proof of Lemma 3:

• If both participation constraints were binding, that is if $\overline{γ}$ and γ were both positive, by construction, the utilitarian expected utility achieved by autarky would be optimal. This has been shown to be impossible, by unicity of the optimum. Thus, one participation constraint necessarily does not bind.

• The first best allocation, which has been proven not to be optimal when ((u(◯)−u(x))/(u(x̄)−u(◯)))⩾((1−θ)E(θ)/θ(1−E(θ)), satisfies the low-risk individual constraint but not that of the high-risk individual.

Therefore, $\overline{γ}$ =0 and γ>0. Then,

 □

Lemma 4

• The Bayesian Incentive constraint for high-risk individuals necessarily binds.

Proof of Lemma 4:

Let us set:

the constraints become respectively: BIC _i (θ)⇔π.δ⩾0, BIC _i (θ̄)⇔ $\overline{π}$ .δ⩽0, PC _i (θ)⇔π.ν=0 and PC _i (θ̄)⇔ $\overline{π}$ . $\overline{ν}$ <0. Moreover we have ν+ $\overline{ν}$ =δ.

Assuming $\overline{λ}$ =0 leads by (A.5) to x ₁(θ, θ, (1, 0))=x ₁(θ, θ, (0, 1)).

As $\overline{λ}$ and λ cannot be simultaneously null, it follows that $\overline{λ}$ ≠0, which implies:

• $\overline{π}$ .δ=0 and thus π.ν+π. $\overline{ν}$ =0. Hence, since π.ν=0, $\overline{π}$ .v=0;

• by (A.6) and (A.7) it follows that:

With

we necessarily would have

This implies:

Recalling x ₁(θ, θ, ω)⩽X(ω)/2⩽x ₂(θ, θ, ω) we have

We hence would have

The right-hand side of the previous inequality is equal to [θ(1−E(θ))(u(x)−u(◯))+(1−θ)E(θ)(u(x̄)−u(◯)) and is therefore positive when (u(◯)−u(x))/(u(x̄)−u(◯))⩽((1−θ)E(θ))/(θ(1−E(θ))). □

We thus end up with a contradiction, meaning that we necessarily have $\overline{λ}$ >0. Therefore, the Bayesian incentive constraint for high-risk individuals binds at the optimum.

Lemma 5

• If preferences are HARA with γ⩾(1/2) then, when ((u(◯)−u(x))/(u(x̄)−u(◯)))⩽((1−θ)E(θ)/θ(1−E(θ)):

  

Proof of Lemma 5:

From Lemma 4 we know that $\overline{λ}$ >0 We are going to show that there is a solution of the optimization program with λ=0. As we know that the solution is unique, the result will follow.

Let us set $\overline{λ}$ >0, λ=0, $\overline{γ}$ =0 and γ>0, which gives:

By setting v ₁≡A/D and v ₂≡A/C the first-order conditions give

Let us first define the function ϕ(·,·) as: u′(2X−ϕ(X, v))/u′(ϕ(X, v))=v. It is easy to show that ϕ(X, ν) is a strictly increasing function with X and ν, with ϕ(X, 1)=X and (2X−ϕ(X, v))=ϕ(X, 1/v). □

Moreover, simple calculations give (we note ϕ _ν and ϕ _X the partial derivatives of ϕ and A(Y) the index of absolute aversion of u at Y):

and

For HARA functions ϕ can be put in the following form:

and

Using this function we have: x ₁(θ̄, θ, (0, 0))=ϕ(x̄, v ₁); x ₁(θ̄, θ, (1, 0))=ϕ(◯, v ₁); x ₁(θ̄, θ, (0, 1))=ϕ(◯, v ₂); x ₁(θ̄, θ, (1, 1))=ϕ(x̄, v ₂); x ₁(θ, θ, (1, 0))=ϕ(◯, v ₁/v ₂); x ₁(θ, θ, (a, a))=X(ω)/2; and x ₁(θ̄, θ̄, ω)=X(ω)/2. Then,

and

we can write π(θ)·δ as π(θ)·δ=(1−θ)[μ P+μ̄ Q]+θ[μ R+μ̄ S] with

(π(θ)·δ=0) then represents the equation (BIC _i (θ)) in the plane (ν ₁, ν ₂).

In the following, we prove that the two Bayesian incentive constraints only cross once (anti-clockwise) in this plane (at the point ν ₁=ν ₂=1).

Noting F _i =∂F/∂v _i and F _X =∂F/∂X, we have (∂(π(θ)·δ)/∂v _i )=(1−θ)[μ P _i +μ̄ Q _i ]+θ[μ R _i +μ̄ S _i ]. Therefore,

The sign of ∂Ω/∂θ is then the sign of [μ P ₂][μ R ₁]−[μ P ₁+μ̄ Q ₁][μ R ₂+μ̄ S ₂] that is the sign of μ ²[R ₁ P ₂−P ₁ R ₂]−μ μ̄[P ₁ S ₂+Q ₁ R ₂]−μ̄ ² Q ₁ S ₂

As P ₁⩽0, Q ₁⩽0, S ₂⩽0, R ₂⩽0, this sign is negative whatever μ if and only if R ₁ P ₂⩽P ₁ R ₂

Letting P=(1−θ)α(x̄, v ₁)+θ β(◯, v ₁, v ₂) and R=(1−θ)γ(◯, ν ₁, ν ₂)+θ δ(x, ν ₂), we obtain

with α ₁⩽0, β ₁⩽0 γ ₂⩽0 δ ₂⩽0

Therefore R ₁ P ₂−P ₁ R ₂ is negative whatever θ; if and only if γ ₁ β ₂−γ ₂ β ₁−α ₁ δ ₂⩽0.

After some tedious computation this amounts to

For which a sufficient condition is

that is

For HARA utility functions u(c)=ξ[η+(c/γ)]^1−γ this writes:

which is verified for ν ₁ and ν ₂ positive when γ⩾(1/2) (this can be proved by showing that, when γ⩾(1/2), the minimum value of the left-hand side is higher than the right-hand side).

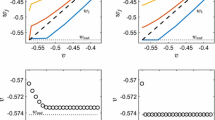
We conclude, then, that when γ⩾(1/2), ∂Ω/∂θ is negative. Therefore, in the plane (ν ₁, ν ₂) the curves (π(θ)·δ=0) and (π(θ̄)·δ=0) cross once at (ν ₁, ν ₂)=(1, 1)

Lastly, we prove that, at the optimum, we necessarily have ν ₂>1.

Under the optimal contract,

and we can easily prove by contradiction that when ((u(◯)−u(x))/(u(x̄)−u(◯)))<(((1−θ)E(θ))/(θ(1−E(θ)))), π(θ)·ν⩾0 → v ₂>1