Abstract
We consider a population of individuals who differ in two dimensions, their risk type (expected loss) and their risk aversion, and solve for the profit-maximising menu of contracts that a monopolistic insurer puts out on the market. Our findings are threefold. First, it is never optimal to fully separate all the types. Second, if heterogeneity in risk aversion is sufficiently high, then some high-risk individuals (the risk-tolerant ones) will obtain lower coverage than some low-risk individuals (the risk-averse ones). Third, because women tend to be more risk averse than men (in that the risk aversion distribution for women first-order stochastically dominates that for men), gender discrimination may lead to a Pareto improvement.
Similar content being viewed by others
Introduction
Individuals who seek insurance differ from each other in many respects. At least two of these differences are of central importance for insurance companies and for insurance market outcomes: the distribution of losses that insurance takers face, and their willingness to bear the risk of those losses.Footnote 1 Empirically, heterogeneity in the second characteristic is not negligible. For example, Aarbu and SchroyenFootnote 2 find that the degree of relative risk aversion among Norwegians averages around 3.7 with a standard deviation of 2.1.
Insurance market theory has primarily focused on the consequences of private information on the loss distribution, and to a lesser extent on the case in which information on risk aversion is private. The study of situations in which private information applies to both characteristics is much more scant.Footnote 3 Moreover, analysis of the two-dimensional private information problem has been restricted to competitive markets; that is, a setting in which several insurers compete for clients. In this paper, we study the opposite setting by asking how a monopolist would design a contract menu intended to attract agents who hold not only private information on their loss distribution, but also on their risk preferences.
Our monopolistic set-up encompasses (admittedly, in an extreme way) the presence of market power in insurance markets. Several empirical studies have recently documented the presence of such market failure or of one of its causes: significant search and switching costs for different lines of insurance. HonkaFootnote 4 estimates the average search cost in U.S. car insurance to lie between USD45 (online quote) and USD110 (offline quote), and the average switching cost at USD85. She argues that these costs may be an important cause for the high customer retention rates in that industry. In their study of a firm offering automobile insurance in Israel, Cohen and EinavFootnote 5 argue that the firm has market power and that a monopoly insurance model better describes this situation than a competitive one. Also, health insurance markets show symptoms of low competitive pressure. In the Swiss health insurance market, premiums exhibit large variability even within the same canton despite coverage being strictly regulated. Indeed, LamiraudFootnote 6 reports that in the Geneva canton the difference between the least expensive insurance contract and the most expensive one amounted to 1,919 in 2011, a difference of 39 per cent. For the U.S. health insurance market, DafnyFootnote 7 provides evidence of direct price discrimination of insurees in local markets, and Bates et al. Footnote 8 find evidence that health insurers do exercise their market power to raise premiums.Footnote 9 Although it is true that several firms may be present in a given geographical area, this does not guarantee a competitive outcome. Several reasons for this market failure have been put forward and shown to be consistent with empirical observations. These include promotion expenditures, first-mover advantages, exclusive control over final service provider networks, and—as already mentioned—switching costs. These switching costs, in turn, could be explained by choice overload (be it cognitive or psychological), status quo bias, bundling of basic and supplemental coverage, or lack of transferability of premium bonuses for low claims during a given period.Footnote 10
Adding risk aversion heterogeneity to the analysis of insurance markets calls for a multidimensional hidden information model. Such an analysis is technically not straightforward because the existence of private information in two or more dimensions implies that the ordering of agents according to their willingness to pay for extra coverage becomes endogenous. In other words, the ordering depends on the contract. To see this, consider two contracts: one with very partial coverage and one with almost full coverage. When offered the former contract, a highly risk-averse agent facing a low risk may be more willing to pay for additional coverage than a risk-tolerant agent facing a high risk, while the situation could be the other way around for the latter contract. Technically, the indifference curves of these “ intermediate” insurance takers cross twice, and this invalidates standard solution methods.Footnote 11
The literature on solutions to multidimensional screening problems is not that wide. One branch of this literature is methodological and deals with a principal–agent setting, as we do—see, for example, the “user’s guide” by Armstrong and Rochet.Footnote 12 It turns out, however, that our insurance problem does not lend itself to being solved by the techniques proposed therein, the main reason being that our problem has two hidden characteristics, but only one instrument—the degree of coverage.Footnote 13 A second branch of literature deals with multidimensional screening in insurance markets, but restricts itself to competitive markets. In this literature, it is usually assumed that each insurance company offers a single contract.Footnote 14 , Footnote 15 In a monopolistic setting such as ours, such a restriction would render the analysis somewhat unrealistic, as market power allows the insurer to screen via menus without the fear of undercutting by rivals. By assuming that the monopolist offers a menu of contracts, the relative proportions of the non-intermediate types play a role that is as crucial as the non-single crossing of intermediate types’ indifference curves. Hence, the problem of the failure of the single-crossing condition—brought about by the intermediate types—is compounded in the monopolistic setting by the necessity of dealing with non-intermediate types in the design of the optimal menu of contracts.
Our main objective is to characterise this optimal menu. We establish three results: (i) it is always optimal to pool some of the types (i.e. full separation of types is never optimal); (ii) unlike in the one-dimensional case, exclusion of some high-risk individuals from insurance may be optimal; and (iii) some low-risk individuals may end up with more coverage than some high-risk individuals.
Next, we address two issues that recently have received much attention. The first one is methodological. In testing for the presence of asymmetric information in insurance markets, the question is whether the absence of significant positive correlation between risk and coverage (i.e. the absence of adverse selection) should be taken as indicative of the absence of asymmetric information. Chiappori et al. Footnote 16 (CJSS henceforth) derive the testable prediction that in a sufficiently competitive insurance market with asymmetric information, the observable risk should be related to coverage in a positive monotone way. Notice that this is stronger than requiring a positive correlation between coverage and risk. We show when this result goes through in our monopolistic setting and when it does not. In the latter case, we also show when risk and coverage can be statistically, positively correlated and when they cannot. In this sense, our results corroborate the role of the sufficient competition assumption for the result in CJSS. Our analysis also adds the combination of market power and preference heterogeneity to the list of possible explanations for the lack of evidence supporting the existence of asymmetric information.Footnote 17 Other explanations in the (growing) list are: (i) endogenous heterogeneity in risks because of moral hazard (see, e.g. Cutler et al. Footnote 18); (ii) endogenous wealth heterogeneity (Netzer and ScheuerFootnote 19); and (iii) the insurer having privileged information on risks (VilleneuveFootnote 20).
The second issue concerns the possible welfare consequences of a ban on the use of gender discrimination in insurance. Such a ban took effect in December 2012 in the European Union, extending to the insurance industry the principle of equal treatment of women and men in the access to and the supply of goods and services.Footnote 21 This will affect the insurance sector, because of the common practice of differentiating premiums according to gender when underwriting life, health and car accident risks. Regarding life insurance, it has been argued that if one controls for lifestyle, environmental factors and social class, “the difference in average life expectancy between men and women lies between zero and two years” and therefore that “the practice of insurers to use sex as a determining factor in the evaluation of risk is based on ease of use rather than on real value as a guide to life expectancy” (p. 6).Footnote 22 We show that even if—as the Commission claims—gender does not provide any information on the underlying risk, if it does provide (imperfect) information on an individual’s risk aversion (as empirical research suggests), then allowing the monopolist to condition the terms of the insurance contract on gender may be Pareto improving. We provide sufficient conditions for such an improvement to arise.
From a technical point of view, we have taken a new approach to the analysis of screening insurance takers that simplifies the problem and is appealing from a modelling point of view. Rather than following the standard set-up in which the individual faces the possibility of a single monetary loss, we assume that the loss is normally distributed and that agents differ in their expected losses, which can be high or low. If the insurance indemnity is linear in the loss, as is the case under a reimbursement scheme with a constant coinsurance rate, final income will also be normally distributed. Endowing agents with a utility function that displays constant absolute risk aversion, which also can be high or low, means that their preferences over uncertain income prospects can be represented as mean-variance preferences. An important consequence of this approach is that preferences over insurance contracts become quasi-linear in the insurance premium and therefore in the information rent. Readers familiar with contract theory will acknowledge the usefulness of linearity in the information rent in specifying the incentive compatibility constraints. An additional advantage of mean-variance preferences is that they allow for an explicit characterisation of the optimal menu of contracts.
The limitations of our approach follow immediately from these assumptions. We do not consider insurance contracts with either a deductible or a cap because such features would destroy the normality of net income. Second, the normality assumption implies a positive likelihood of negative losses, although this problem may be rendered of secondary importance by considering sufficiently high means and/or low variances for the losses. Perhaps the most important objection is that we have no skewness in the loss distribution, and in particular no strictly positive probability mass for a zero loss. Nevertheless, these are minor limitations when compared with the considerable advantages the approach offers for characterising the solution to a two-dimensional screening problem.
The remainder of the paper is organised as follows. In the next section, we model the preferences of insurance takers and specify reimbursement contracts. In the subsequent section, we set up the problem faced by a monopolistic insurer. In the section “One-dimensional screening”, we characterise the optimal menu of contracts when insurees only differ in risk levels or risk aversion, as well as considering the case of perfect positive correlation. In the section “Two-dimensional screening”, we assume that insurees differ in both respects simultaneously and discuss the five menus that may be optimal. We determine which menu is dominating for which part of the parameter space. In the section “The positive correlation test”, we interpret the testable prediction of CJSS in the light of our results. In the subsequent section, we trace out the consequences of allowing the monopolistic insurer to gender discriminate. The final section concludes.
Except when otherwise stated, we have relegated all proofs to a technical companion paper that is on the Geneva Risk and Insurance Review’s website.
Insurance takers and reimbursement contracts
Insurance takers
We assume that individuals are endowed with initial wealth e and a negative exponential von Neumann–Morgenstern utility function defined on final wealth y: u(y)=−exp(−ry), where r>0 is the (constant) degree of absolute risk aversion. Initial wealth is subject to a random loss z that follows a normal distribution with mean μ and variance σ 2.
Agents have access to reimbursement insurance. A typical reimbursement contract pays out a compensation of 1−c per euro loss, in return for a premium P. Ex post, final wealth is then given by

which ex ante is also normally distributed. We will express a contract C as a pair of a coinsurance rate c and a premium P: C=(c, P).
Under the assumptions made, the certainty equivalent (CE) wealth function takes the mean-variance form: U=E(y)−(r/2)var(y). By replacing the mean and variance of final wealth, CE wealth is given by:

From now on, we write  and assume that this product can be either high or low, and likewise for the expected loss: μ∈{μ
L
, μ
H
} and ν∈{ν
L
, ν
H
}, where μ
L
<μ
H
and ν
L
<ν
H
. The model can thus be interpreted in two ways: either individuals are equally risk averse but their losses have different variances, or the loss variance is identical but individuals have different degrees of risk aversion. Throughout, we adhere to the second interpretation and will refer to ν as risk aversion.
and assume that this product can be either high or low, and likewise for the expected loss: μ∈{μ
L
, μ
H
} and ν∈{ν
L
, ν
H
}, where μ
L
<μ
H
and ν
L
<ν
H
. The model can thus be interpreted in two ways: either individuals are equally risk averse but their losses have different variances, or the loss variance is identical but individuals have different degrees of risk aversion. Throughout, we adhere to the second interpretation and will refer to ν as risk aversion.
A person with characteristics (μ i , ν j ) is said to be of type ij. The share of ij individuals in the population is given by α ij (i, j=H, L, ∑ i, j α ij =1). We denote by α k⋅ the fraction of individuals with expected loss μ k (α k⋅ =α kL + α kH ); similarly, α ⋅k is the fraction of individuals with risk aversion ν k (α ⋅k =α Lk +α Hk ).
Incentive compatible contracts
When a person of type ij (i, j∈{H, L}) signs the contract C=(c, P), her CE wealth is

If instead she decides to remain uninsured, her CE wealth becomes e−μ i −(1/2)ν j , which is equivalent to accepting the degenerate contract (c, P)=(1, 0). The CE rent that the agent enjoys from contract (c, P) is then

Hence, the rent decreases with the coinsurance rate both via the expected loss and via risk aversion (if c>0).
The marginal willingness to pay for a slightly lower coinsurance rate c is

which increases linearly in c.
Indifference curves in the contract space (c, P) are thus concave in c, and downward sloping for non-negative coinsurance rates. In addition, individuals with higher expected losses and/or greater risk aversion have a higher marginal willingness to pay. Figure 1 illustrates the indifference curve that passes through the no-insurance point N=(1, 0). Given that the slope of the indifference curve when it passes the P-axis is μ, it is easy to decompose the total willingness to pay for full insurance into the expected loss and the risk premium ν/2.
When agent ij signs a contract intended for agent kl, the rent that the former receives is given by:

It is useful to define the following function:

Suppose now that type kl is truthful and receives rent R kl (c kl , P kl ). Which rent does ij obtain when choosing the contract for kl? Using (1) and (3), the answer is given by:

Thus, by pretending to be type kl, type ij can obtain type kl’s rent plus δ.
To see the usefulness of contract distortion, let us fix the rent that a truthful type kl receives under the contract (c kl , P kl ). A marginal increase in the coinsurance rate for kl, dc kl >0, then needs to be accompanied by a marginal decrease in the premium, dP kl =(μ k +c kl ν l )dc kl . This has the following effect on the rent for the mimicker ij:

Thus, the rent for ij goes down to the extent that ij is mimicking a type with a lower risk or with lower risk aversion. Intuitively, when raising the co-payment of a low-risk (or risk-tolerant) individual, the decrease in the premium needed to compensate him is not too large, because of the small likelihood of needing that co-payment (or because of the low valuation of the increase in the variance of final wealth). However, a person with a higher risk level or greater risk aversion who is tempted by this contract will dislike this change. Thus, increasing a co-insurance rate for some types will lower the rents of all those mimicking (and the mimickers of these mimickers) who have a higher risk, and will increase the rent of all those mimicking (and the mimickers of these mimickers) who have lower risk aversion.
From now on, we simply write R ij for R ij (c ij , P ij ) (i, j=L, H). Self-selection between contracts (c ij , P ij ) and (c kl , P kl ) then requires that

which, taken together, imply 0⩾δ(c kl , μ i −μ k , ν j −ν l )+δ(c ij , μ k −μ i , ν l −ν j ), or, using (3),

A necessary condition for incentive compatibility between contracts for Hj and Lj (j=H, L) is that

with  Similarly, incentive compatibility between contracts iH and iL (i=H, L) requires that
Similarly, incentive compatibility between contracts iH and iL (i=H, L) requires that

with  and where it is assumed that c⩾0 (on which more below).
and where it is assumed that c⩾0 (on which more below).
The double dimensionality leads in general to double crossing of the indifference curves of types HL and LH. Solving MWP
HL(c)=MWP
LH(c) for c yields c=(Δμ/Δν). That is, in the (c, P) space, the locus of tangency points between HL’s and LH’s indifference curves is a vertical line at Δμ/Δν. For lower coinsurance rates, HL’s indifference curve crosses that of LH downwards from above, while for higher rates, this happens from below. The quadratic expressions for CE wealth ensure that if a crossing occurs at a rate c
− to the left of Δμ/Δν, then the second crossing occurs at c
+, at the same distance to the right of Δμ/Δν (see Figure 2). Hence, if we say that the indifference curves of HL and LH form a lens, then (c
++c
−)/2=Δμ/Δν is the position of this lens, while  is its size.Footnote 23
is its size.Footnote 23
Next, we introduce two crucial variables for characterising the profit maximising set of contracts:

The ratio D measures, in a unit-free fashion, the difference in risk between two types.Footnote 24 The ratio x measures the degree of similarity along the risk-aversion dimension. Using this notation, the locus of tangency points is therefore located at Dx/(1−x), so that for sufficiently small x, the tangency of the intermediate types’ indifference occurs at a coinsurance rate below unity. This makes it possible that both crossings become relevant for the analysis.
The insurance company
We consider a single, risk-neutral insurer with monopoly power on the market for reimbursement contracts. Her expected profits when an agent of type ij has accepted a reimbursement contract (c, P) is given by:

Therefore, the iso-profit associated with type ij has slope −μ i in the contract space (c, P).
With full information, the monopolist will provide ij with full insurance (c ij =0) at a premium that sets her rent equal to zero. Hence, using (1), P ij =μ i +(1/2)ν j . This yields a per capita payoff equal to π=(1/2)ν j . The tangency line in Figure 1 thus corresponds to the highest feasible iso-profit line, and the profit that the insurer makes can be read off from the dashed vertical axis on the right-hand side. Under full information, the insurer can extract the entire risk premium ν/2. In what follows, we will characterise the optimal coinsurance rates and the optimal rents. The corresponding premiums can then be found with the help of (1).
Given (6), the insurer’s total profit is equal to ∑ i, j α ij π ij(c ij , P ij ). From (1) and (6)—both evaluated at (c ij , P ij )—and recalling that we can write R ij for R ij (c ij , P ij ) (i.e. type ij’s rent when truthful), we can express the insurer’s total profit as ∑ i, j α ij [(1/2)[1−c ij 2]v j −R ij ]. This objective function is to be maximised with respect to (c ij , R ij ) (ij=H, L), subject to the usual voluntary participation and incentive compatibility constraints.
As in most of the literature, to these constraints we add two additional sets of constraints that are needed to avoid false claims (see, e.g. PicardFootnote 25). If a coinsurance rate is negative, the insurer refunds more than 100 per cent of the losses, and the insuree will obviously have a strong incentive to overstate the size of the loss. On the other hand, if a coinsurance rate exceeds unity, the agent will have to be paid to accept such a contract (i.e. a negative premium). Once the agent has accepted the insurance, he would have to pay the insurer as well as bearing the loss once it occurs. It is clear that he would have strong incentives to understate the size of the loss (or even hide the loss altogether). Hence, we constrain coinsurance rates to lie in the interval [0, 1].
The monopolist thus solves the following problem:

The first set of constraints ensures voluntary participation, while the second ensures that all types self-select. The third set comprises the (reduced form) ex ante and ex post moral hazard constraints.
The following theorem provides the usual result of no-distortion-at-the-top (full insurance for the HH type) and no-rents-at-the-bottom.
Theorem 1
-
At the optimum, (i) c HH =0 and (ii) R LL =0.
Before characterising the rest of the solution to the two-dimensional screening problem, it is useful to first consider the one-dimensional case.
One-dimensional screening
There are three instances in which screening becomes unidimensional. In the first instance, all agents have the same risk aversion; that is, ν H =ν L =ν. This is the standard monopoly problem with just two types when insurees either bear a low or a high expected loss. The type distribution can be described by a single parameter α H⋅, the proportion of high risks in the population. We have the following theorem.
Theorem 2
-
When all agents have the same risk aversion, the optimal menu has c H⋅=0 and c L⋅=min{Dα H⋅/(1−α H⋅), 1}.
The full insurance contract giving L zero rent would be selected by H as well. At a zero coinsurance rate, the slope of H’s indifference curve is steeper than that of L. If the insurer increases c L⋅ above zero, this will create a second-order reduction in profit from L, but a first-order gain in profit from H, because the latter can be charged a strictly higher premium (for full insurance). Hence, it pays to start distorting L’s contract. The optimal coinsurance rate balances the gain in profit from H (α H⋅Δμ) with the loss in profits from L ((1−α H⋅)ν). Notice that it may pay to exclude type L whenever α H⋅⩾1/(1+D); that is, whenever the proportion of low loss agents is sufficiently small—as expected.
The second instance in which the screening problem becomes unidimensional is when individuals differ in risk aversion only. Let α ⋅H instead be the proportion of highly risk averse types; that is, those with ν=ν H (>ν L ). We have the following theorem.
Theorem 3
-
When all agents face the same expected loss, the optimal menu has c ⋅H =0, and

This result is less standard. With only differences in risk aversion, the optimal solution is always at the corner. Either the low type is excluded or he receives full insurance. The reason for this “bang-bang” solution is that, unlike in the different risk scenario, at a zero coinsurance rate, both H’s and L’s indifference curves are tangential to one another. Hence, distorting L’s contract by raising the coinsurance rate now results in a second-order gain in profit from H, and it is the second-order condition that determines whether c ⋅L =0 is a local maximum or minimum.
The final instance of unidimensional screening arises when risk levels and risk aversion are perfectly positively correlated. As it transpires from (2), we have MWP HH(c)>MWP LL(c) for any c. The two types are therefore once again unambiguously ordered.
Theorem 4
-
When the two characteristics are perfectly positively correlated, the optimal menu has c HH =0 and

We now turn to the two-dimensional screening problem.
Two-dimensional screening
From now on, we let individuals not only differ in their risk levels, but also in their risk aversion. The insurance company then faces the following bivariate probability distribution of types:

The correlation between risk (μ) and risk aversion (ν) is given by

In what follows, we let ρ represent the numerator of the correlation expression: viz.,  and refer from now on to ρ as the degree of correlation; it plays a central role in the analysis.
and refer from now on to ρ as the degree of correlation; it plays a central role in the analysis.
To parameterise the distribution of types, we use the triplet (α H⋅, α HH , ρ), and have the remaining fractions determined by


and

Non-negativity of α LH and α LL requires that −α HL (1−α H⋅)⩽ρ⩽α HH (1−α H⋅). The feasible set of distribution parameters is then

The other parameters of the model, D and x, pertain to the characteristics of the insurance takers. This part of the parameter space is denoted as the types set 

It turns out that D and x are sufficient to describe the problem—we can discard the original parameters μ i and ν j (i, j=H, L).Footnote 26
In our analysis, we focus on the case in which the correlation of characteristics is non-positive (ρ⩽0). Arguably, this is the most empirically relevant situation: highly risk-averse individuals tend to take more precautions and are thereby less likely to experience losses. Our model could be seen as a reduced form of a more general model in which individuals have initially taken such precautions before going to the insurance market. The second reason for this restriction on the sign of ρ is pragmatic: under negative correlation, the typology of the equilibrium set of contracts is already complex, but mostly invariant to the degree of negative correlation. By contrast, with positive correlation, the degree of correlation starts to matter for characterising the optimal contract menus in the parameter space. Thus, we restrict the set of distribution parameters to

The monotonicity conditions (4) and (5) imply that there are only two possible orderings of coinsurance rates:

At an optimal solution, the contracts of the different types are linked by a chain of incentive compatibility constraints. Under Order 1, HH should then be indifferent between her own contract and at least that for HL. The next lemma (proven in the appendix) shows that HL is either pooled with HH or with LH.
Lemma 1
-
Suppose Order 1 applies with c HH <c LH . Then it is optimal to pool HL with HH if x>(α HH /α H⋅ ); otherwise HL should be pooled with LH.
This result follows from Theorem 3. With Order 1, the only type who may want to mimic HL is HH. Thus, the choice of c HL is only governed by weighing the profits from these two types. Because they have the same risk levels, we can apply Theorem 3 to this subgroup. Given that the fraction of highly risk-averse individuals in this group is α HH /α H⋅, the result follows. Thus no menu having Order 1 will have full separation of types.
Suboptimality of full separation is also the case in Order 2. This follows from the following lemma (proven in the appendix).
Lemma 2
-
Suppose that Order 2 applies. Suppose also that (i) HH is indifferent between her own contract and that for LH, but strictly dislikes that for HL; (ii) LH is indifferent between her own contract and that for HL, but strictly dislikes that for LL; and (iii) HL is indifferent between her own contract and that for LL. Then, profit can be increased by pooling HL with either LL or LH.
Before presenting our main result, we introduce the following upper bound on the heterogeneity in risks

and in the remainder of the paper, we restrict the parameter space as

In this way, it will never turn optimal to exclude type LL and therefore any other type under an Order 1 menu.Footnote 27 We will later comment on how our results change when risk heterogeneity is larger than 
We now define five menus that may turn optimal for values in the parameter space  They are listed in Table 1, and distinguished as to whether the degree of separation of the low-risk types, measured as c
LL
−c
LH
, is larger or smaller than the size of the lens formed by the indifference curves of HL and LH (ℓ). Columns 3 and 4 in the table refer to the optimal coinsurance rates and the x-range for which the menu is optimal. If a coinsurance rate is not mentioned in column 3, it is because it is equal to zero (full insurance).
They are listed in Table 1, and distinguished as to whether the degree of separation of the low-risk types, measured as c
LL
−c
LH
, is larger or smaller than the size of the lens formed by the indifference curves of HL and LH (ℓ). Columns 3 and 4 in the table refer to the optimal coinsurance rates and the x-range for which the menu is optimal. If a coinsurance rate is not mentioned in column 3, it is because it is equal to zero (full insurance).
Menu A pools the high-risk types at full insurance, and the low-risk types at high, but partial, insurance. Figure 3 illustrates. (In this figure and those that follow, solid/dashed indifference curves refer to high/low risk aversion, while bold/thin indifference curves refer to high/low risks).
This policy corresponds to one under which individuals differ only in their risk dimensions (Theorem 2). If x⩾1−α LL >α H⋅, which we shall argue below is the optimal range to make use of A, the pooling of the low-risk types happens at a “low” coinsurance rate, viz., c L· A<Dx/(1−x)(=Δμ/Δv).
In menu B, the two low-risk types are separated by positioning them on each side of the lens. That is, they satisfy c LH +c LL ≡2Dx/(1−x). We may distinguish between menu Bf and menu Bp, depending on whether LH obtains full insurance (c LH =0) or partial insurance (c LH >0), respectively. The two panels of Figure 4 illustrate.
Menu C is a menu where everybody is fully insured, except for the LL individuals who face a very high coinsurance rate. Moreover, the screening between LH and LL is now very thorough in the sense that c LL −c LH >ℓ. Consequently, c LL ⩾2Δμ/Δν. Menu C thus balances a high premium income from the “ upper” types with the loss in profit from severely distorting LL’s contract. Intuitively, with few LL individuals around, such distortion is attractive. This menu is illustrated in Figure 5.
A common feature of all previous menus is that Order 1 applies (c HL ⩽c LH ). In menu E, the opposite is true: HL’s contract is now severely distorted by being pooled with LL. This makes room for increasing the distortion on LH, which, in turn, allows the insurer to extract more rent from HH individuals. If there are few low risk-averse individuals around, it may pay to exclude these individuals from the market (EX), otherwise they are included but receive limited insurance (EI). Figure 6 illustrates.
In menu E, separation of LH from LL is once more weak: c LL −c LH <ℓ. Under Order 1, separation of LL from LH is carried out to increase the profits from HH, HL and LH at the cost of a lower profit from LL. Under Order 2, HL is pooled with LL so as to extract more rent from the highly risk-averse types, HH and LH. Across these two types, rent extraction is optimised in the standard way (cf. Theorem 2).
We now provide the main result of the paper. It refers to the distribution space  which for the time being is sufficient to describe as almost as big as
which for the time being is sufficient to describe as almost as big as  We comment on the difference between
We comment on the difference between  and
and  later.
later.
Proposition 1
-
Suppose that
 Then, the optimal menu structure as a mapping from
Then, the optimal menu structure as a mapping from  into the menu set is as illustrated in
Figure 7
. For each menu, the optimal coinsurance rates are as given in
Table 1.
into the menu set is as illustrated in
Figure 7
. For each menu, the optimal coinsurance rates are as given in
Table 1.
The formal proof is in the technical companion paper that is on the Review’s website; a sketch of the “proof strategy” is given in the appendix. Here, we restrict ourselves to a heuristic explanation of Proposition 1. Suppose that x equals 1 (no heterogeneity in risk aversion). Then it is optimal to design the menu as if there were only two groups—low- and high-risk people—which is exactly what menu A does: the high-risk types obtain full insurance while the low-risk types face a co-insurance rate as prescribed by Theorem 2. When x falls below 1, ν H starts to exceed ν L . This makes it optimal to start screening the LL from the LH types: by providing LL with less coverage (at a lower premium), LH (and therefore also the high-risk types HH and HL) can be charged a higher premium. However, because LL was initially pooled with LH at the left-hand crossing, a marginal increase in c LL is impossible for incentive compatibility reasons (see Figure 3). What is possible is to move LL from the left-hand crossing to the coinsurance rate corresponding to the right-hand crossing, and adjusting her premium to keep her rent at zero. This non-marginal “reform” involves a big loss in profit from LL and will only be compensated by a larger profit from the “upper” types when x<1−α LL ; then, menu Bp takes over.
From the expression for c LH Bp it is easy to verify that ∂c LH Bp/∂x>0 and therefore that ∂c L Bp/∂x<0. Thus, more heterogeneity in risk aversion (lower x) calls for distorting LH’s contract less and LL’s contract more. This process goes on until also LH is provided with full insurance (at x=(1+α LH −α LL )/(1+α LH +α LL )). This is where we enter menu Bf. It can be shown that the maximal profit under menu Bf is a function of x that is inverse U-shaped, with a maximal profit reached at x=(1−α LL )/(1+α LL ). For lower x—that is, larger risk aversion heterogeneity—this maximal profit can be secured by switching to menu C which keeps on providing full insurance to the “upper” types but no longer insists on having LL at the right-hand crossing of the lens, as menus Bp or Bf do. The wedge between c LL and c LH now starts to exceed ℓ. The maximal profit of C is independent of x. See Figure 8 for the maximal profits as functions of x and the appendix for their specification.
As explained earlier, a common feature of all menus of Order 1 is that HL insurees are provided with at least as much coverage as LH insurees. At the same time, the incentive compatibility constraints between these two types require that the order can only be reversed by providing far less coverage to HL than to LH. This is costly, because HL agents, despite their low risk aversion, have a large willingness to pay for being relieved from the high risk they face. It is when risk aversion heterogeneity gets very large that the benefit of reversing the order outweighs this cost: although LH agents face a low risk, their excessive risk aversion (and that of HH) endows them with a large risk premium which the insurer wants to extract. This is when it pays off to reverse the order and substitute menu E for menu C. In the technical companion paper that is on the Review’s website, we show that there exists a function, x CE (α H⋅,α HH , ρ, D), non-increasing in D, such that π E>π C⇔x<x CE (α H⋅, α HH , ρ, D).
We conclude the discussion of Proposition 1 with three remarks.
Remark 1
-
The transition between the menus of Order 1 is continuous in the sense that at least one of the coinsurance rates of the lower types is continuous in x. However, the optimal coinsurance rates show a discontinuity in x when Order 1 is replaced by Order 2. This is illustrated in Figure 9 depicting the optimal values of c LL and c LH as a function of x. Thus x CE (α H⋅, α HH , ρ, D) is found by direct comparison of the maximal profit under menu C with the maximal profit under menu E.Footnote 28
Remark 2
-
Because there is continuity when switching from B to C, whereas there is discontinuity when switching from C to E, one may wonder whether π E may exceed π C for any x that makes C dominate B. In other words, does it make more sense to compare π E with π B? This is illustrated in Figure 8. The profit function π E intersects with π C at
 while the function
while the function  dominates π
C, indicating that once x falls short of
dominates π
C, indicating that once x falls short of  menu B should be replaced by menu E. In the appendix, we substantiate the following claim:
menu B should be replaced by menu E. In the appendix, we substantiate the following claim:
Claim 1
-
The subset of distributions (α H⋅, α HH , ρ) in
 for which menu
C
is entirely dominated by menus
B
and
E
is almost negligible. In particular, if ρ⩽−0.089, there does not exists a feasible pair (α
H⋅, α
HH
) where this is the case.
for which menu
C
is entirely dominated by menus
B
and
E
is almost negligible. In particular, if ρ⩽−0.089, there does not exists a feasible pair (α
H⋅, α
HH
) where this is the case.
In other words, the set  mentioned in Proposition 1 is almost as large as the distribution set
mentioned in Proposition 1 is almost as large as the distribution set 
Remark 3
-
So far, we have restricted the heterogeneity in risk (D) below
 . Recall that D measures the incentive for μ
H
-type individuals to mimic μ
L
-type individuals, normalised by (twice) the risk premium of the latter. A high coinsurance rate on μ
L
-types discourages μ
H
-types from applying for the contracts intended for the latter, and thus allows insurers to charge the former group more for full insurance. For D exceeding
. Recall that D measures the incentive for μ
H
-type individuals to mimic μ
L
-type individuals, normalised by (twice) the risk premium of the latter. A high coinsurance rate on μ
L
-types discourages μ
H
-types from applying for the contracts intended for the latter, and thus allows insurers to charge the former group more for full insurance. For D exceeding  it will turn optimal to start excluding LL types. In the appendix, we have redrawn Figure 7 for D∈[0, (1−α
H⋅)/α
H⋅].Footnote 29 The only new difference w.r.t. Figure 7 is that a new menu labelled M appears as a slice in between menus A and B. This menu excludes LL type as well, but has a degree of separation lower than that of B and higher than that of A (0<c
LL
M−c
LH
M<ℓ).
it will turn optimal to start excluding LL types. In the appendix, we have redrawn Figure 7 for D∈[0, (1−α
H⋅)/α
H⋅].Footnote 29 The only new difference w.r.t. Figure 7 is that a new menu labelled M appears as a slice in between menus A and B. This menu excludes LL type as well, but has a degree of separation lower than that of B and higher than that of A (0<c
LL
M−c
LH
M<ℓ).
This concludes the discussion of the optimal menu choice. In the next two sections, we will discuss the implications for testing for the presence of asymmetric information and the normative implications for banning gender discrimination.
The positive correlation test
CJSS16 showed that a common prediction of any model of a competitive insurance market with asymmetric information is a strictly positive relationship between the degree of coverage and the expected loss across contracts. This is quite a strong result, and we refer to it as positive monotonicity (PM). This property implies a positive correlation between coverage and risk, but the converse is of course not true.
In the empirical literature on testing for asymmetric information in insurance markets, researchers typically rely on estimating the correlation coefficient between coverage and the expected loss, and then use a one-sided test to determine whether this coefficient is statistically significantly positive (see, e.g. Cohen and SiegelmanFootnote 30; Finkelstein and McGarryFootnote 31). The empirical evidence on positive correlation is somewhat weak; there is even evidence of negative correlation in some markets.Footnote 32 This is quite surprising because the result of CJSS is general; conditional on the competition assumption, it holds for any combination of moral hazard and adverse selection in underlying risk.Footnote 33
As mentioned in the introduction, several theoretical explanations for this lack of evidence have been proposed. One is the so-called “cherry picking argument” (Chiappori and SalaniéFootnote 34) or “propitious selection” (HemenwayFootnote 35), which combines adverse selection in risk preference (but not in the underlying risk) with moral hazard. The argument is that, if individual A is more risk averse than B, then A is willing to purchase more coverage than B. But, being more risk averse, A may ex post take more precautions than B. This may then result in a negative correlation between observed risk and coverage.Footnote 36
Because the optimal menu in a monopoly market with two-dimensional screening may display Order 2, PM will cease to hold; for a subset of types (LH and HL), coverage is negatively related to risk size. This of course does not imply that the correlation between risk and coverage is negative, because PM does hold for other subsets of types (between HH on the one hand, and LH and LL on the other). This also suggests that a sufficiently negative correlation between risk and risk aversion (i.e. a sufficiently negative ρ) ensures a negative correlation between coverage and risk size. This is shown below.
Also CJSS point out that the PM property may be violated in a monopoly. They do this by starting with a model in which only preference heterogeneity exists (cf. the section “One-dimensional insurance”), and then introduce an infinitesimal amount of exogenous risk heterogeneity that is perfectly negatively correlated with risk aversion heterogeneity (i.e. the more risk-averse agents have a slightly smaller accident probability). Below, we show that the PM property does not hold whenever menu E applies, even if the underlying risk and risk preference are independently distributed.
Translated into our setting, the CJSS proposition may be stated as follows:
Consider two contracts C a and C b that are offered on the market. Suppose that: (i) C a gives more coverage then C b , that is, c a <c b ; and (ii) the per capita profit generated by contract a does not exceed that of contract b, π(C a )⩽π(C b ). Then, (iii) the expected loss to those consumers signing up for contract a should exceed the expected loss of those consumers signing up for contract b, that is, μ(C a )⩾μ(C b ).
It is easy to see that property (iii) is satisfied in all menus except for menu E. In that menu, the contract for LH has more coverage than the contract for the low risk-averse individuals (LL and HL). The PM property would then require that μ(C LH )=μ L >μ(C ⋅L )=μ H (α HL /α ⋅L )+μ L (α LL /α ⋅L ), which is obviously violated. The culprit is the violation of condition (ii): C LH E generates a higher per capita profit than does C ⋅L E. Indeed,

Because C LH E<C ⋅L E, it follows that π(C LH )>π(C ⋅L ), irrespective of which optimal values the coinsurance rates take under menu E.
Performing a positive correlation test on our model would amount to calculating the covariance across contracts between 1−c(C) and μ(C):

As the second part of the following proposition shows, when the optimal menu is EI, this covariance is negative if and only if the correlation between expected loss and risk aversion, ρ, is sufficiently negative.
Proposition 2
-
(i) For a sufficient degree of heterogeneity in risk aversion, such that menu E prevails, some low-risk individuals (LH) purchase more coverage than do some high-risk individuals (HL). (ii) In the case of menu EI , cov(1−c(C ij ), μ(C ij ))<0 if and only if ρ<−α HH (x−α HH /α H⋅) (<0).
In other words, the advantageous selection among LH and HL, described by part (i), may exactly offset the standard adverse selection, such that any correlation between risk and coverage vanishes. Finkelstein and McGarry31 show that the long-term care insurance market may suffer from asymmetric information, despite the absence of evidence for a positive correlation between risk and coverage. Our model helps in interpreting this evidence.
Gender discrimination
Crocker and SnowFootnote 37 have shown that imperfect categorical discrimination in insurance—such as gender discrimination—always expands the efficiency frontier. HoyFootnote 38 showed how categorisation based on a signal may lead to a Pareto improvement in a competitive insurance market if the signal conveys information about the level of risk. In this section, we ask when such efficiency gains arise in a monopolistic market structure. We show that a Pareto improvement is possible if the signal, such as gender, is informative about risk aversion.
Let us write p(μ, ν, g) as the likelihood function that an arbitrary insuree has an expected loss of μ, risk aversion of ν and gender g∈{m, w}. A monopolist who is allowed to condition on gender will, for each gender g, design an optimal contract menu based on the risk-aversion ratio x, the risk difference parameter D, and the probability matrixFootnote 39

We now assume that risk aversion is a sufficient statistic for gender with respect to the expected loss:

Condition S means that within a given risk-aversion class, the observation of a person’s gender carries no extra information about the risk class to which this person belongs.Footnote 40 In general, sufficiency is not enough to break the link between gender and expected loss. If female drivers are highly risk averse, and if this attitude leads them to careful driving, then there will still be a connection between gender and expected loss. This last connection is broken by the assumption that expected loss is independently distributed of risk aversion—that is, risk aversion has no impact on driving. This allows us to state the following result.
Lemma 3
-
If the likelihood function p(⋅) satisfies Condition S and if μ and ν are independently distributed, then μ and g are also independently distributed: p(μ|g)=p(μ).
Thus, these assumptions support the conclusion reached by the European Commission—that gender is insignificant in explaining risk type.
Because a gender-discriminating firm will use the probability functions p(μ, ν|g) (g=m, w), rather than the single function p(μ, ν), to design menus, and because profits and consumer rents depend on the coinsurance rate c LL , it is important to determine the effect of p(⋅) on c LL . From Proposition 1, it follows that without discrimination, the upper boundaries of menus C, Bf and Bp are determined by the parameters α LL and α LH . Fixing x and α L⋅ (and therefore α H⋅=1−α L⋅) allows one to trace out the optimal value of c LL as a function of α LL .Footnote 41 This yields Figure 10, in which it is assumed that (1−x)/(1+x)<(1/2)(1+α L⋅)(1−x). This means that the curve for LL’s optimal coinsurance rate is flat for some range of α LL values; this is equivalent to assuming that

This condition is satisfied when the proportion of low-risk individuals, α L⋅, is not too small in relation to x.
There is ample evidence that men are on average less risk averse than women.Footnote 42 For our model, this means that p(ν L |w)<p(ν L )<p(ν L |m). An insurance company that is allowed to gender discriminate, having observed the customer’s gender g, will update the probability α LL in the following way:

where the first equality sign follows from Condition S and the second follows from independence. Thus, while α L⋅ and α H⋅ do not change when gender is observed, α LL does.
Suppose now that (12) holds, and suppose that the proportion of LL individuals as a whole, among men and among women, is α LL , α LL|m , and α LL|w , respectively. Suppose also that these proportions are as illustrated in Figure 11.
Then, we can conclude that, because

the coinsurance rate for LL women will remain at its no-discrimination value, and the rents of LH women, HL women, and HH women will not change because of discrimination (and LL women continue to receive zero rent). On the other hand, because

the optimal coinsurance rate for LL men will drop below its no-discrimination value, and therefore, all men will receive more rent when offered the optimal contract menu for men (except LL men, who continue to receive zero rent).Footnote 43 The insurance company will increase its total profits because it prefers to choose a new menu for its male clientele—it could have stuck to the same menu as in the no-discrimination case. Thus, a Pareto improvement is possible by allowing gender discrimination. As can be seen from the figure, conditions (13) and (14) are not only sufficient for a Pareto improvement, but also necessary. We summarise this result in the following proposition.
Proposition 3
-
Suppose that Condition S holds, and that μ and ν are independently distributed. Suppose that (12) holds. For given values of x, α L⋅ , and D, allowing gender discrimination will lead to a Pareto improvement in the insurance market if and only if conditions (13) and (14) hold.
Intuitively, because men are on average less risk averse, the “male” market consists of more LL types than does the overall market. This makes the distortion of the LL contract that was optimal for the entire market too costly for the “male” market: offering LL men a lower coinsurance rate (in return for a higher premium) increases profits from this market segment sufficiently to compensate for the lower rents extracted from the “higher” male types. Hence, all men benefit, and so does the monopolist.
It is worth mentioning that a similar result can be derived in the case where risk-averse and risk-tolerant agents all face the same expected loss.Footnote 44 Then the optimal menu has c ⋅H =0, while c ⋅L =1 if and only if x⩽α ⋅H (or α ⋅L ⩽1−x) (cf. Theorem 3). In other words, all types receive full insurance—which implies that risk-averse agents receive a rent—except if risk-tolerant individuals are sufficiently few in number. In this latter case, risk-tolerant agents are excluded and the risk-averse ones receive no rent. Hence, if one starts from a situation with few risk-tolerant agents (and where no agent obtains any rents), gender discrimination may create a “male” market with sufficiently many risk-tolerant agents so that these no longer become excluded. This in turn raises the rents of risk-averse men in that market. The “female” market is not affected since gender discrimination leads to an even lower percentage of risk-tolerant women, reinforcing the optimality of their exclusion. This result can be illustrated using a figure analogous to Figure 11, now with α ⋅L on the horizontal axis and c ⋅L on the vertical axis. The curve depicting c ⋅L is flat at 1 to the left of point 1−x and jumps down to zero to the right of 1−x. Starting from an overall proportion α ⋅L to the right of 1−x, gender discrimination may result in α ⋅L|w <1−x<α ⋅L|m , and thus in a Pareto improvement.
Conclusion
In this paper, we studied the outcome in a monopolistic insurance market when the insurer is only aware of the statistical distribution of the expected loss and the level of risk aversion of its customers. We formulated a mean-variance model that results in quasi-linear preferences over contracts; we identified the five contract menus that emerge in equilibrium; and for each menu, we derived the optimal co-insurance rates. Next, we identified for each menu the subset of parameter values for which that menu is optimal. We did this under non-positive correlation between the two characteristics.
We found that
-
it is never optimal to fully separate all the types. In other words, there will always be some pooling of types in equilibrium;
-
the greater is the heterogeneity in the expected loss, the more it pays to screen the low-risk from the high-risk types, by imposing a high coinsurance rate on the former;
-
the greater is the heterogeneity in terms of risk aversion, the more it pays to screen the low risk averse from the highly risk averse by imposing a high coinsurance rate on the former; and
-
the property of positive monotonicity between coverage and expected loss need no longer hold—neither does the property of positive correlation.
We also identified an open set of parameter values such that when the female distribution of risk aversion first-order stochastically dominates the male distribution, allowing gender discrimination results in a Pareto improvement in this market. Hence, our analysis shows that one should be careful when abolishing gender categorisation; even when gender itself does not (statistically) affect the expected level of losses or claims, it may affect the outcome in an imperfectly competitive insurance market so that nobody gains and some participants become worse off.
Notes
A third factor, that will not be discussed here, is the moral stance of insurees, determining the amount of false claims that insurers have to deal with each year.
Rothschild and Stiglitz (1976) analyse a perfectly competitive insurance market with private information on the distribution of losses. Stiglitz (1977, Sections 3 and 4), and Landsberger and Meilijson (1996) analyse a monopolist insurer. Stiglitz (1977, Section 5) and Landsberger and Meilijson (1994) analyse the outcomes under monopoly when private information is held on risk attitude. The latter paper shows that the first best (full extraction of consumer surplus by the insurer) can be achieved arbitrarily close through a very non-linear contract. High risk-averse agents receive their certainty equivalent wealth; low risk-averse agents get, with probability, almost 1 of slightly more than their certainty equivalent, but receive with a tiny probability a very negative wealth. For the more risk-averse agent, this second contract is unattractive. Hence, full insurance with almost complete extraction of the risk premiums is achieved.
Dafny et al. (2012) find that mergers leading to an increase in market concentration were associated to a 7 per cent increase in premiums.
Jullien et al. (2007) analyse whether the single-crossing property holds in the general monopolistic screening model with moral hazard and in which agents differ in their risk preferences. See also De Donder and Hindriks (2009).
Armstrong and Rochet (1999) consider an agent with quasi-linear and separable preferences over two action levels and a transfer. The principal has similar preferences but she does not know whether the agent has a high or low valuation for either of the two activities. A contract specifies a transfer and two activity levels. Thus they have a “two instruments, two common values” problem (see also Dana, 1993). Our problem has only one instrument, that is, insurance coverage. The agent’s willingness to pay for coverage depends on both her risk level and risk aversion. On the other hand, the insurer’s willingness to offer coverage depends on the level of risk, but not on the agent’s risk aversion. Risk aversion only indirectly determines contract profitability through the rents that must be left for incentive compatibility reasons. Thus our problem is of the “one instrument, one common value” type. This also makes our problem different from that of Armstrong (1999) (one instrument and two common value characteristics).
In one-dimensional screening models, competition in menus has been considered by, for example, Miyazaki (1977) and Spence (1978) using the Wilson (1977) equilibrium concept.
This de facto means that the main results are driven by the lack of order between what we refer to as “intermediate types”, that is, by those whose indifference curves cross twice. This explains why some authors only consider these intermediate types (e.g. Wambach, 2000). Although Smart (2000) and Villeneuve (2003) consider the full set of types, they maintain the assumption that each company offers a single contract per risk class. In some models with multidimensional private information, it is possible to reduce the dimensionality by a so-called type aggregator—see, for example, De Donder and Hindricks (2007) for a political economy social insurance context. In a context closer to ours, Crocker and Snow (2011) assume that an insurance taker may face different perils (fire, theft, etc.). Since the probability for each kind of loss is private information, the insurer must engage in multidimensional screening. Because risk classification based on observables is assumed sufficiently fine, the problem can be reduced to single dimensional private information.
CJSS propose a local argument for a negative correlation between risk and coverage to arise in the case of monopoly. Our analysis provides instead a full characterisation.
Council Directive 2004/113/EC of 13 December 2004 implementing the principle of equal treatment between men and women in the access to and supply of goods and services (Official Journal of the European Union 2004 L 373, p. 37). Originally, this directive provided for a derogation that allowed member states to permit gender-specific differences in insurance premiums and benefits in so far as gender is a determining risk factor that can be substantiated by relevant and accurate actuarial and statistical data. In March 2011, however, the European Court of Justice declared this derogating provision in the Directive to be invalid on the grounds that the use of risk factors based on sex in connection with insurance premiums and benefits is incompatible with the principle of equal treatment for men and women under European Union Law (European Court of Justice, 2011).
We have
 . Hence, the size of the lens is
. Hence, the size of the lens is  , a dimensionless number.
, a dimensionless number.Because the coefficient of absolute risk aversion (r) measures twice the risk premium per unit of variance, we can conclude that the risk premium of a low-risk-averse type (RP L , say) equals (1/2)ν L . Therefore, D=Δμ/(2RP L )=(Δμ/μ L )/(2RP L /μ L ).
This is because (i) we can normalise ν L to unity, and (ii) in the monopolist problem only Δμ matters—see (7).
Under Order 2, exclusion of risk-tolerant types will turn optimal, even for small values for D.
It is the lower root of a quadratic equation in x.
(1−α H⋅)/(α H⋅) is the largest value for D for which menu A will still offer coverage to the low-risk types (cf. Theorem 2).
The later phenomenon is termed “ advantageous or propitious selection”. In regard to life insurance, see, for example, Cawley and Philipson (1999) and McCarthy and Mitchell (2003), and in regard to long-term care, see, for example, Finkelstein and McGarry (2006). Olivella and Vera-Hernández (2013) show that, in duplicate private health insurance systems (in which the public and the competitive private insurance sectors offer the same portfolio of services), if heterogeneity is in risks only then propitious selection into private insurance should be observed if and only if information on risks is symmetric.
Moral hazard can encompass two distinct phenomena. One relates to better-covered individuals having less of an incentive to undertake precautionary behaviour, which makes them observationally more risky. The other arises because one does not necessarily observe actual risk but the usage of, say, health services. Because coverage implies a lower cost of accessing these services, individuals may use more of these services because they have more coverage, not because they are more risky. Notice that both types of moral hazard reinforce the positive correlation. Of course, one of the econometric issues is that, even after observing some positive correlation, it is hard to disentangle the adverse selection and either of the two moral hazard effects.
See, for example, Jullien et al. (2007); De Donder and Hindriks (2009); and Finkelstein and McGarry (2006).
We assume that the support of the distribution of types does not vary with the signal. Alternatively, the support could be made dependent on the signal. This, in effect, amounts to assuming that the support consists of more than four (μ, ν) pairs, some of which have zero probability mass, depending on the observation of the signal.
Two equivalent formulations of Condition S are: p(g|μ, ν)=p(g|ν) and p(μ, ν|g)=p(μ|ν)⋅p(ν|g).
By Lemma 3, the marginal probability distribution of the risk size (α L⋅, α H⋅) is fixed.
Because the optimal menu for men is of the type Bp, the rents are given as follows: R HH =R HL +1/2Δν, R HL =R LL +(1−c LL )Δμ, R LH =R LL +(1/2)(1−c LL 2)Δν, and R LL =0. Since c LL falls under discrimination, R ij (ij≠LL) rises.
We thank the Editor, Achim Wambach, for pointing this out to us.
Since x CE (α H⋅, α HH , ρ, D) is decreasing in D, it is sufficient to consider x CE (α H⋅, α HH , ρ, D)|small D .
That is, if (α H· , α HH )∈
 (ρ) for some ρ⩽0, then (α
H·
, α
HH
, ρ)∈
(ρ) for some ρ⩽0, then (α
H·
, α
HH
, ρ)∈ .
.
References
Aarbu, K.O. and Schroyen, F. (2014) Mapping risk aversion in Norway using hypothetical income gambles, discussion paper 13/09 (revised January 2014), Norwegian School of Economics.
Armstrong, M. (1999) ‘Optimal regulation with unknown demand and cost functions’, Journal of Economic Theory 84 (2): 196–215.
Armstrong, M. and Rochet, J.C. (1999) ‘Multi-dimensional screening: A user’s guide’, European Economic Review 43 (4–6): 959–979.
Bates, L., Hilliard, J. and Santerre, R. (2012) ‘Do health insurers possess market power?’, Southern Economic Journal 78 (4): 1289–1304.
Cawley, J. and Philipson, T. (1999) ‘An empirical examination of information barriers to trade in insurance’, American Economic Review 89 (4): 827–846.
Chiappori, P.A., Jullien, B., Salanié, B. and Salanié, F. (2006) ‘Asymmetric information in insurance: General testable implications’, Rand Journal of Economics 37 (4): 783–798.
Chiappori, P.A. and Salanié, B. (2000) ‘Testing for asymmetric information in insurance markets’, Journal of Political Economy 108 (3): 56–78.
Cohen, A. and Einav, L. (2007) ‘Estimating risk preferences from deductible choice’, American Economic Review 97 (3): 745–788.
Cohen, A. and Siegelman, P. (2010) ‘Testing for adverse selection in insurance markets’, The Journal of Risk and Insurance 77 (1): 39–84.
Commission of the European Communities. (2003) ‘Proposal for a Council Directive implementing the principle of equal treatment between women and men in the access to and the supply of goods and services’, Council Directive 2003/657.
Crocker, K. and Snow, A. (1986) ‘The efficiency effects of categorical discrimination in the insurance industry’, Journal of Political Economy 94 (2): 321–344.
Crocker, K. and Snow, A. (2011) ‘Multidimensional screening in insurance markets with adverse selection’, The Journal of Risk and Insurance 78 (2): 287–307.
Cutler, D., Finkelstein, A. and McGarry, K. (2008) ‘Preference heterogeneity and insurance markets: Explaining a puzzle of insurance’, American Economic Review 98 (2): 157–162.
Dafny, L. (2010) ‘Are health insurance markets competitive?’, American Economic Review 100 (4): 1399–1431.
Dafny, L., Duggan, M. and Ramanarayanan, S. (2012) ‘Paying a premium on your premium? Consolidation in the U.S. health insurance industry’, American Economic Review 102 (2): 1161–1185.
Dana, J. (1993) ‘The organization and scope of agents’, Journal of Economic Theory 59 (2): 288–310.
De Donder, P. and Hindriks, J. (2007) ‘Equilibrium social insurance with policy-motivated parties’, European Journal of Political Economy 23 (3): 624–640.
De Donder, P. and Hindriks, J. (2009) ‘Adverse selection, moral hazard and propitious selection’, Journal of Risk and Uncertainty 38 (1): 73–86.
Eckel, C. and Grossman, P.J. (2008) ‘Men, women and risk aversion’, in C. Plott and C. Smith (eds.), Handbook of Experimental Economics Results, vol. 1, ch. 113, Amsterdam: North-Holland.
European Court of Justice. (2011) Press release No 12/11, from http://curia.europa.eu/jcms/jcms/P_72733, accessed on 5 March 2011.
Finkelstein, A. and McGarry, K. (2006) ‘Multiple dimensions of private information: Evidence from the long-term care insurance market’, American Economic Review 96 (4): 938–958.
Hartog, J., Ferrer-i-Carbonell, A. and Jonker, N. (2002) ‘Linking measured risk aversion to individual characteristics’, Kyklos 55 (1): 3–26.
Hemenway, D. (1990) ‘Propitious selection’, Quarterly Journal of Economics 105 (4): 1063–1069.
Honka, E. (2010) ‘Quantifying search and switching costs in the U.S. auto insurance industry’, mimeo, Booth School of Business, University of Chicago.
Hoy, M. (1982) ‘Categorizing risks in the insurance industry’, Quarterly Journal of Economics 97 (2): 321–336.
Jullien, B., Salanié, B. and Salanié, F. (2007) ‘Screening risk averse agents under moral hazard: Single-crossing and the CARA case’, Economic Theory 30 (1): 151–169.
Kimball, M., Sahm, C. and Shapiro, M. (2008) ‘Imputing risk tolerance from survey responses’, Journal of the American Statistical Association 103 (483): 1028–1038.
Lamiraud, K. (2014) ‘Switching costs in competitive health insurance markets’, in T. Culyer (ed.), Encyclopedia of Health Economics, Amsterdam: Elsevier.
Landsberger, M. and Meilijson, I. (1994) ‘Monopoly insurance under adverse selection when agents differ in risk aversion’, Journal of Economic Theory 63 (2): 392–407.
Landsberger, M. and Meilijson, I. (1996) ‘Extraction of surplus under adverse selection: The case of insurance markets’, Journal of Economic Theory 69 (1): 234–239.
McCarthy, D. and Mitchell, O. (2003) International adverse selection in life insurance and annuities, NBER working paper 9975.
Miyazaki, H. (1977) ‘The rat race and internal labour markets’, Bell Journal of Economics 8 (2): 394–418.
Netzer, N. and Scheuer, F. (2010) ‘Competitive screening in insurance markets with endogenous wealth heterogeneity’, Economic Theory 44 (2): 187–211.
Olivella, P. and Vera-Hernández, M. (2013) ‘Testing for asymmetric information in private health insurance’, Economic Journal 123 (567): 96–130.
Picard, P. (2000) ‘Economic analysis of insurance fraud’, in G. Dionne (ed.), Handbook of Insurance, New York: North-Holland, p. 2000.
Rothschild, M. and Stiglitz, J. (1976) ‘Equilibrium in competitive insurance markets: An essay on the economics of imperfect information’, Quarterly Journal of Economics 90 (4): 629–649.
Smart, M. (2000) ‘Competitive insurance markets with two unobservables’, International Economic Review 41 (1): 153–169.
Spence, M. (1978) ‘Product differentiation and performance in insurance markets’, Journal of Public Economics 10 (3): 427–447.
Stiglitz, J. (1977) ‘Monopoly, non-linear pricing and imperfect information: The insurance market’, Review of Economic Studies 44 (3): 407–430.
Villeneuve, B (2000) ‘The consequences for a monopolistic insurer of evaluating risk better than customers: the adverse selection hypothesis reversed’, The Geneva Papers on Risk and Insurance Theory 25 (1): 65–79.
Villeneuve, B. (2003) ‘Concurrence et antisélection multidimensionelle en assurance’, Annales d'Économie et de Statistique 0 (69): 119–142.
Wambach, A. (2000) ‘Introducing heterogeneity in the Rothschild–Stiglitz model’, The Journal of Risk and Insurance 67 (4): 579–591.
Wilson, C. (1977) ‘A model of insurance markets with incomplete information’, Journal of Economic Theory 16 (2): 167–207.
Acknowledgements
We are grateful to two anonymuous referees and the editor (Achim Wambach) for their detailed comments and suggestions. The paper has benefited from presentations at various seminars and conferences: Boston University, CORE (Louvain-la-Neuve), ECARES (Brussels), HECER (Helsinki), NHH (Bergen), Toulouse School of Economics, the 6th European Health Economics Workshop, the 6th Public Economic Theory Meeting, the 5th IHEA World Congress, the 33rd EGRIE meeting, the 2009 HEB-HERO Health Economics Workshop. Particular thanks to Catarina Goulão, Jean Hindriks, Eirik Kristiansen, Eric Nævdal and Gaute Torsvik for discussions and comments. Olivella acknowledges support from the Government of Catalonia project 2005SGR00836 and the Barcelona GSE Research Network, as well as from the Ministerio de Educación y Ciencia, project ECO2012–31962 and CONSOLIDER-INGENIO 2010 (CSD2006–0016). Schroyen acknowledges the hospitality of CODE (Universitat Autónoma de Barcelona) where this project was started, and CORE (Université catholique de Louvain) where this version was completed, and financial support from Health Economics Bergen through an SNF grant.
Author information
Authors and Affiliations
Additional information
Supplementary Information accompanies this paper on the The Geneva Risk and Insurance Review website (http://www.palgrave-journals.com/grir)
Electronic supplementary material
Appendix
Appendix
The approach to prove Proposition 1
At an abstract level, for any  the problem is:
the problem is:

where m is a contract menu (C
HH
, C
HL
, C
LH
, C
LL
) and  is the set of feasible menus satisfying the self-selection and participation constraints. Problem (A.1) is complex both due to the number of inequality constraints that define the feasible set, and because this set is beset by non-convexities. To identify the solution for each
is the set of feasible menus satisfying the self-selection and participation constraints. Problem (A.1) is complex both due to the number of inequality constraints that define the feasible set, and because this set is beset by non-convexities. To identify the solution for each  we proceed as follows.
we proceed as follows.
First, we delineate the set of incentive compatible menus as much as possible by deriving a list of properties that any optimal incentive compatible menu should satisfy. This allows us to restrict the feasible set to a reduced set  such that
such that

Second, we identify three subsets  (i=1, 2, 3), with
(i=1, 2, 3), with  but not necessarily with empty intersections. This allows us to define solutions to three sub-problems:
but not necessarily with empty intersections. This allows us to define solutions to three sub-problems:  (i=1, 2 3). Because the three subsets unite to
(i=1, 2 3). Because the three subsets unite to  it follows that
it follows that

Third, we solve each of the three sub-problems. Finally, we perform a comparison to distinguish the global solution from the local ones. For this comparison, we rely on the following revealed preference principle:

Two of the three subproblems belong to Order 1. The third belongs to Order 2. To identify the partitioning of  where Order 2 takes over from Order 1, a direct comparison of the maximal value functions will turn necessary.
where Order 2 takes over from Order 1, a direct comparison of the maximal value functions will turn necessary.
Proof of Lemma 1
-
The proof goes by contradiction. That is, suppose that Order 1 applies and that the optimal menu has c HH <c HL <c LH . We adopt the following notation: ij→(↛)kl means that ij gets as much (more) rent out of her own contract than out of the contract for kl.
-
1
From Lemma 8 in the technical companion paper that is on the Review’s website, we know that at an optimal solution either HH→HL or HH→LH or both. If “both”, Corollary 1 in that paper tells that c HL =c LH , contradicting the assumption. If HH →LH and HH↛HL, then R HH =R LH +δ(c LH , Δμ, 0)>R HL +δ(c HL , 0, Δν). Since R HL ⩾R LH +δ(c LH , Δμ, −Δν), it follows that R LH +δ(c LH , Δμ, 0)>R LH +δ(c LH , Δμ,−Δν)+δ(c HL , 0, Δν), or c HL >c LH contradicting the assumption. Hence, the only possibility that is left is HH→HL and HH↛LH.
-
2
Suppose that LH→HL. Then R LH =R HL +δ(c HL ,−Δμ, Δν) and R HL ⩾R LH +δ(c LH , Δμ,−Δν) imply that either c LH =c HL or that c HL <c LH ⩽2(Δμ/Δν)−c HL . The first possibility is ruled out by assumption. The second possibility means that c LH is between c HL and the right-hand crossing of the lens. See Figure A.1.
-
3
Recall from step 1 that HH↛LH. Suppose now that LL→ LH. Then R LL =R LH +δ(c LH , 0,−Δν). But this means that by reducing c LH down to the left-hand crossing of the lens, LL’s rent when mimicking LH is reduced (∂(R LH +δ(c LH , 0,−Δν))/∂(−c LH )<0). Thus reducing c LH to the left-hand crossing of the lens is feasible without upsetting LL’s incentive compatibility constraint. Hence, if LH→HL then we must have that at an optimal solution the contracts for HL and LH are located at the left-hand crossing of the lens, contradicting that c HL <c LH . Therefore, LH↛HL.
-
4
If c HL <c LH , then LL↛HL. Suppose on the contrary that LL→HL. Then R LL =R HL +δ(c HL ,−Δμ,0). But self-selection of LL requires R LL ⩾R LH +δ(c LH , 0,−Δν). Therefore R HL +δ(c HL ,−Δμ, 0)⩾R LH +δ(c LH , 0,−Δν). However, self-selection of LH requires R LH ⩾R HL +δ(c HL ,−Δμ, Δν). Combining both inequalities gives δ(c HL ,−Δμ, 0)⩾δ(c LH , 0,−Δν)+δ(c HL ,−Δμ, Δν) or c HL ⩾c LH . Since c HL <c LH by assumption, we have a contradiction.Summing up so far: only HH is tempted by the contract for HL.
-
5
By increasing c HL , only the rent of HH will be affected (lowered). The rents of LH and LL are unaffected. Hence, the motivation for increasing c HH is based on balancing the reduction of HH’s rent with the increase in the distortion of HL’s contract. It follows then from Theorem 3 that it is either optimal to set c HL equal to c HH (when x>α HH /α H⋅) or to increase c HL as much as possible. Since we argued in step 2 that the upper bound is the left-hand crossing where LH is located, it follows that when x<α HH /α H⋅, it is optimal to set c HL =c LH .
□
-
1
Proof of Lemma 2
-
The proof goes by contradiction. Suppose that full separation under Order 2 is optimal. This situation is depicted in Figure A.2.
First note that c LL must exceed Δμ/Δν=Dx/(1−x) because, otherwise, LH and HL could not have been separated.
The profits from the different types are as follows:

Weighting with the respective population proportions gives the following first derivatives with respect to the coinsurance rates.

The solution for c LL is c LL =min{D(1−α LL )/α LL , 1}. A necessary condition that c LL <Dx/(1−x) is x<1−α LL . Only if c LL >Dx/(1−x) is there room to separate LH from HL. Because

total profit is strictly concave in c HL if and only if x⩾α ⋅H /(1−α LL ). In that case, the optimal solution for c HL is c HL =min{Dα ⋅H x/(α ⋅H (1−x)−α HL x), 1}.
By monotonicity, the only possibility for full separation arises when c HL =Dα ⋅H x/(α ⋅H (1−x)−α HL x)<1. It remains then to check whether c HL <c LL . Suppose first that c LL =D(1−α LL )/α LL <1. Then,

Because α ⋅H (1−α LL )/(α ⋅H α LL +(1−α LL )2)<α ⋅H /(1−α LL ), this condition contradicts the assumption that x⩾α ⋅H /(1−α LL ). Suppose next that c LL =1. Then,

Again, this contradicts the assumption that x⩾α ⋅H /(1−α LL ). Hence, c HL =c LL , meaning that HL is pooled with LL.
On the other hand, if total profit is strictly convex in c HL , it pays to move c HL either down to c LH or up to c LL . Hence, full separation is never optimal. □
The maximal profit functions for each menu
For menus A, Bp and Bf, the profits from the four types are as follows:

and total profit is

For menu A, upon substitution for the optimal coinsurance rates, the maximal profit function becomes

Using the optimal coinsurance rates for menu Bp gives

while using the optimal coinsurance rates for menu Bf gives

In the case of menu C, the profits from the four types are

and total profit is

Replacing c LL with the optimal coinsurance rate for menu C gives

Finally, the profits under menu E are given by

Hence, total profit is

Inserting the optimal coinsurance rates for this menu gives

“Proof” of Claim 1
For each value of ρ(⩽0), we can define a region  (ρ) in the (α
H⋅, α
HH
) space such that the profit function for menu E is depicted by
(ρ) in the (α
H⋅, α
HH
) space such that the profit function for menu E is depicted by  rather than π
E in Figure 8
Footnote 45:
rather than π
E in Figure 8
Footnote 45:

Bundles in this region can be shown to be feasible.Footnote 46 Figure A.3(a)-(c) displays  (ρ) for ρ=0, (−1/30), (−2/30). Thus, if ρ=(−2/30), then for almost all (α
H⋅, α
HH
) that are feasible in combination with this value for ρ (the area delineated by the dashed line), it transpires that the interval for which menu C is optimal, [x
CE
(α
H⋅, α
HH
, ρ, D), min{(1−α
LL
(α
H⋅, α
HH
, ρ))/(1+α
LL
(α
H⋅, α
HH
, ρ)), 1/(1+2D)}], is non-empty. For ρ⩽−0.089, “almost all” can be replaced by “any”.
(ρ) for ρ=0, (−1/30), (−2/30). Thus, if ρ=(−2/30), then for almost all (α
H⋅, α
HH
) that are feasible in combination with this value for ρ (the area delineated by the dashed line), it transpires that the interval for which menu C is optimal, [x
CE
(α
H⋅, α
HH
, ρ, D), min{(1−α
LL
(α
H⋅, α
HH
, ρ))/(1+α
LL
(α
H⋅, α
HH
, ρ)), 1/(1+2D)}], is non-empty. For ρ⩽−0.089, “almost all” can be replaced by “any”.
We therefore restrict the set of distribution parameters further to

However, from the previous discussion,  is almost as large as
is almost as large as 
The extension of Proposition 1 when D∈[0, (1−α H⋅)/α H⋅]
First note that (1−α H⋅)/α H⋅ is the maximal value for D such that the low-risk types LL and LH are pooled at a coinsurance rate below 1 under menu A.
Second, if D is large, then under menu A, the right-hand crossing will happen at a coinsurance rate exceeding 1 and at a negative premium. To establish separation of LL from LH, LL can be excluded, while the premiums for LH and the high-risk types are increased with an amount to make LH indifferent between having insurance at the original coinsurance rate c L⋅ and being uninsured. This increase in premia is (1/2)(1−c L 2)v H , yielding a profit increase of (1−α LL )(1/2)(1−c L· 2)v H . The loss in profit by excluding the LL types is α LL (1/2)(1−c L· 2)v L . The gain exceeds the loss whenever x < 1 − α LL . The new menu we end up with is menu M. It gives full insurance to HH, a small but positive coinsurance rate for LH, but exclusion of LL. Type HL is pooled with HH if x>α HH /α H⋅; otherwise, this type is pooled with LH (cf. Lemma 1). Figure A.4 (drawn for x>α HH /α H⋅) illustrates this menu.
The optimal values for the coinsurance rates under M are given by


Thus, the difference between A and M is that the low-risk types (LH and LL) are now separated from one another, but the degree of separation is “small”, in the sense that c LL −c LH <ℓ, the size of the lens.
Figure 7 of Proposition 1 can now be extended as in Figure A.5. In this figure, the postscripts I and X are attached to menus Bp and C to distinguish whether type LL is included (c LL <1) or excluded (c LL =1). As shown in Lemma 1, whether HL is pooled with HH or with LH depends on whether x exceeds or falls short of α HH /α H⋅. A sufficient condition for HL being pooled with HH in menus M and BpX is

Figure A.5 is drawn for on α H⋅=0.6, α HH =0.2 and ρ=0. Hence, this sufficiency condition is satisfied, and all (D, x) combinations in the regions for BpX and M have pooling of HL with HH rather than with LH. □
Proof of proposition 2, part (ii)
Under menu EI, c HH E=0, c LH C=Dxα HH /α LH and c ·L E=Dxα HL /(x−α ·H ), with x>α ⋅H =α LH +α HH . (see Table 1, “row” EI). Using the definition of α LH (Eq. (9)), the inequality condition on x is equivalent to x>(α HH /α H⋅)−(ρ/α H⋅). Therefore,

In addition, ρ⩽0 is necessary and sufficient for α HH /α H⋅⩽α ⋅H . Thus x>α ⋅H and ρ⩽0 imply

Substituting the expressions for the optimal coinsurance rates in the covariance formula (11) and making use of the formulae for α HL , α LH and α LL (8)–(10), allows us to write the covariance between coverage and risk as

Given (A.3), all the terms in the round brackets in the above expression are positive. From (A.2), the denominator is positive. Therefore,

Rights and permissions
About this article
Cite this article
Olivella, P., Schroyen, F. Multidimensional Screening in a Monopolistic Insurance Market. Geneva Risk Insur Rev 39, 90–130 (2014). https://doi.org/10.1057/grir.2014.1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/grir.2014.1


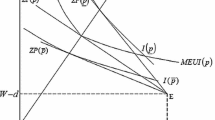









 Then, the optimal menu structure as a mapping from
Then, the optimal menu structure as a mapping from  into the menu set is as illustrated in
into the menu set is as illustrated in 
 Regime C is entirely dominated by Regime E.
Regime C is entirely dominated by Regime E.
 while the function
while the function  dominates π
C, indicating that once x falls short of
dominates π
C, indicating that once x falls short of  menu B should be replaced by menu E. In the
menu B should be replaced by menu E. In the  for which menu
C
is entirely dominated by menus
B
and
E
is almost negligible. In particular, if ρ⩽−0.089, there does not exists a feasible pair (α
H⋅, α
HH
) where this is the case.
for which menu
C
is entirely dominated by menus
B
and
E
is almost negligible. In particular, if ρ⩽−0.089, there does not exists a feasible pair (α
H⋅, α
HH
) where this is the case.
 . Recall that D measures the incentive for μ
H
-type individuals to mimic μ
L
-type individuals, normalised by (twice) the risk premium of the latter. A high coinsurance rate on μ
L
-types discourages μ
H
-types from applying for the contracts intended for the latter, and thus allows insurers to charge the former group more for full insurance. For D exceeding
. Recall that D measures the incentive for μ
H
-type individuals to mimic μ
L
-type individuals, normalised by (twice) the risk premium of the latter. A high coinsurance rate on μ
L
-types discourages μ
H
-types from applying for the contracts intended for the latter, and thus allows insurers to charge the former group more for full insurance. For D exceeding  it will turn optimal to start excluding LL types. In the
it will turn optimal to start excluding LL types. In the 

 . Hence, the size of the lens is
. Hence, the size of the lens is  , a dimensionless number.
, a dimensionless number. (ρ) for some ρ⩽0, then (α
H·
, α
HH
, ρ)∈
(ρ) for some ρ⩽0, then (α
H·
, α
HH
, ρ)∈ .
.







 .
.
