INTRODUCTION

Systemic risk is the risk that affects not just specific market participants, but an entire financial market or system due to the interlinkages and interdependences of financial institutions throughout the world. Federal Reserve Chairman Ben Bernanke in a letter to the chair of the US Senate Banking Committee on 30 October 2009 defined systemic risk as follows: ‘Systemic risks are developments that threaten the stability of the financial system as a whole and consequently the broader economy, not just that of one or two institutions’. Policy measures to address systemic risk associated with ‘systemically important financial institutions’ was published by the Financial Stability Board in November 2011. Two years later, that organization published a list of 29 banks that is categorized as ‘globally systemically important banks’.

There exist several methodologies to assess and evaluate when a country, a firm and/or a financial institution become distressed (see, among others, Jensen, 1989; Doumpos et al, 2001; Kosmidou et al, 2008; Cohen et al, 2012; Clare et al, 2013; and Strub, 2013). In particular, the study and management of systemic risk is a fundamental part of the literature on volatility models, tail risk and contagion risk. Adrian and Brunnermeier (2011), Segoviano and Goodhart (2009), Zhou (2010), and Ergun and Girardi (2013), among others, try to assess how financial institutions become distressed when another financial institution is in distress. Several authors have proposed systemic risk measures (see, for example, Adrian and Brunnermeier, 2011; Adams et al, forthcoming; Wong and Fong, 2010; Gauthier et al, 2012; and Cao, 2013). The measure that has received a fair amount of attention is the one proposed by Adrian and Brunnermeier (2011) in a Staff Report for the Federal Reserve Bank of New York, ‘CoVaR’ with ‘VaR’ standing for the commonly used risk measure value-at-risk measure and ‘Co’ denoting the first two letters in conditional, contagion and comovement.Footnote 1 They argue that any measure of systemic risk should be called co-measures, should account for comovements and contagion, and should be conditional on the behavior among the returns series. CoVaR is then defined as the VaR of the financial system that is conditional on financial systems being in distress. In turn, they define the difference between the CoVaR of a financial institution being in financial distress and the CoVaR in the median state of the financial institution as a financial institution’s contribution to systemic risk.

Although the proposed systemic risk measures have been helpful to global bank regulators, asset managers are seeking guidance for a measure of a portfolio’s systemic risk. The need for such guidance has been highlighted by the recent financial crisis that has emphasized the difficulties of achieving diversification in the face of systemic risk. Not all the risk measures currently used by asset managers in portfolio construction are able to account for systemic risk. The classical (Markowitz) mean-variance portfolio selection approach, for example, does not consider systemic risk since it suggests diversifying the portfolio among those assets that present lower variance and higher mean which makes them more interconnected and thus it could increase the intrinsic systemic risk.

In this article, we propose a reward-risk performance measure based on co-measures of risk and reward. Then we identify the daily optimal asset allocation that maximizes these measures and perform an ex-post empirical analysis of the final portfolio wealth. The new performance measure is essentially a modification of the Rachev ratio (see Biglova et al, 2004) where instead of the average value at risk (AVaR), we propose using the Co-Expected Tail Loss (CoETL). In particular, we define a portfolio’s CoETL as the average of the portfolio losses when all the assets are in distress. For this reason, the CoETL is a good candidate to measure the portfolio downside risk in the presence of systemic risk. Thus, when we use the CoETL measure we take into account all those market collapses (systemic or otherwise) where all the assets are in distress. Clearly, any market collapse event (as are most of the ‘tail events’; see, among others, Clare et al (2013) and Strub (2013)) requires a very large number of observations to be properly measured and, in practice, we almost never have a sufficient number of historical observations for a consistent CoETL measure estimate (as in the case of many others ‘tail’ measures). Therefore, we suggest estimating CoETL by generating a sufficiently large number of realistic scenarios. In particular, we propose maximizing the new performance measure applied to the simulated scenarios.

Although the return distribution assumed in the traditional theories of asset pricing and portfolio selection is the normal distribution, numerous studies that have investigated the empirical behavior of asset returns in financial markets throughout the world reject this distribution (see, for example, Rachev and Mittnik, 2000 and Rachev et al, 2007). Any assumed return distribution must take into account three stylized facts regarding asset returns. First, they are asymmetric and heavy tailed, where the tails are important because bad news represent tail events. The normal distribution is symmetric and the tails are too light to match market data. Typically to overcome this problem, Markov processes such as Lévy processes are used to describe asset returns because they allow for heavy tails and skewness (see, among others, Rachev et al, 2007 and Kim et al, 2008). Second, there is volatility clustering in time series (that is, calm periods followed by highly volatile periods and vice versa). For this reason, GARCH-type processes with Markov residuals have been typically used in financial modeling (see Duan et al, 2006 and Biglova et al, 2009a, 2009b). Third, a dependence structure for a multivariate distribution is needed rather than a simple linear correlation. The dependence model has to be flexible enough to account for several empirical phenomena observed in the data, in particular asymmetry of dependence during severe market crashes and dependence of tail events. The dependence model implied by the multivariate normal distribution fails to describe both phenomena: covariance is a symmetric dependence concept and tail events are asymptotically independent.

As suggested in Biglova et al (2009a, 2009b), we can take into account heavy tailness, volatility clustering and multivariate dependency structure of the return series by using an ARMA(1, 1)-GARCH(1, 1) model with stable distributed innovations and modeling dependencies with an asymmetric Student t copula valued on those innovation series. Therefore, once we generate the future scenarios for equity indexes in our study, we compare the ex-post sample paths of the wealth obtained by maximizing either the Sharpe ratio or the new performance measure (based on the CoETL) applied to the simulated returns. Finally, we compare the optimal portfolio compositions among the different portfolio strategies and then evaluate the impact of transaction costs for the different strategies.

The article is organized as follows. In the next section we introduce the new performance measures. In the subsequent section we analyze the data set. The methodology employed to build scenarios based on a simulated copula is then described, followed by a comparison among different strategies in the penultimate section. Our conclusions are summarized in the final section.

PERFORMANCE MEASURES IN THE PRESENCE OF SYSTEMIC RISK

In this section we introduce a new performance measure that accounts for the presence of systemic risk.

Suppose we have a frictionless market in which no short selling is allowed and all investors act as price takers. Given a benchmark with log-return r b and n risky securities with a vector of log-returns r=[r1,…,r n ]′, the classical portfolio selection problem in the reward-risk framework consists of minimizing a given risk measure ρ provided that the expected reward v is constrained by some minimal value m. The benchmark return r b could be a risk-free return or another specified benchmark. In the empirical comparison reported in the next section we use the log return of the world MSCI index. Among the efficient choices obtained by varying the value of the constraint m, there is a portfolio (commonly referred to as the market portfolio) that provides the maximum expected reward v per unit of risk ρ. Therefore, assuming that the reward and risk are both positive, the market portfolio is obtained as the solution to the following optimization problem:

where the vector notation x′r=∑i=1nx i r i stands for the returns of a portfolio with composition x=[x1,…,x n ]′, and the no short selling assumption is represented by x i ⩾0;∀i. Starting from the original Markowitz’ analysis, Sharpe suggested that investors should maximize the so-called Sharpe ratio (see Sharpe, 1994) given by:

In the Sharpe ratio, risk is proxied by the standard deviation STD(x′r−r b ) of excess returns. Thus, by maximizing the Sharpe ratio, we obtain a market portfolio that is not dominated in the sense of second-order stochastic dominance which should be optimal for non-satiable risk-averse investors.

The behavioral finance literature suggests that most investors are clearly non-satiable (that is, prefer ‘more’ than ‘less’) but their attitude towards risk is not precisely identified and they are neither risk averse nor risk seeking (see, among others, Friedman and Savage, 1948; Markowitz, 1952; Tversky and Kahneman, 1992; Levy and Levy, 2002). Therefore, several performance measures have been proposed and used in portfolio theory to capture the different perception of reward and risk (see Rachev et al, 2008). In this article, we propose another performance measure able to capture the presence of systemic risk that is based on the same idea of reward and risk of the Rachev ratio (see Biglova et al, 2004).

The Rachev ratio is the ratio between excess return portfolio’s AVaRs as follows:

where r b is a benchmark return. AVaR, also known as Conditional Value-at-Risk (CVaR), is defined as:

where VaRq(X)=−F X −1(q)=−inf{x|P(X⩽x)>q} is the VaR of the random return X and 1−α is the confidence level of the average of X losses (that is, VaRs). If we assume a continuous distribution for the probability law of X, then AVaR α (X)=−E(X|X⩽−VaR α (X)) and, therefore, AVaR α can be interpreted as the average loss beyond its α-percentile. Moreover, AVaR α of the negatively signed random variable (−X) is the average of the gains greater than its (1−α)-percentile (that is, AVaR α (−X)=E(X|X⩾−VaR1−α(X))) and thus it represents a particular reward measure. Moreover, when we maximize the Rachev ratio we obtain a choice that is optimal for non-satiable investors who are neither risk averse, nor risk seeking and whose attitude towards risk is identified by the parameters α and β.

In order to account for the presence of systemic risk in the portfolio selection problem, we suggest using as a co-measure of risk the average of the portfolio losses when all the assets are in distress, a measure that we refer to as CoETL, that is:

This measure evaluates the losses during periods of financial system instability caused by idiosyncratic events for all assets. For this reason, CoETL is able to evaluate a portfolio’s systemic risk. Moreover, it has been observed that in financial markets prices are often found to increase together. We can take into account this behavior of asset prices using as a co-reward measure the mean of the portfolio return when all the assets are increasing in value, a measure we refer to as co-Expected Tail Profit, that is:

Therefore, in order to account for the comovements of losses and profits, we propose the following extension of the Rachev ratio, that we call the Co-Rachev ratio:

EMPIRICAL EVIDENCE

In this section, we analyze the stock indexes used in the following portfolio empirical analysis. We use stock indexes of the first 14 developed countries (as classified by MSCI barra) with the highest nominal GDP according to the International Monetary Fund (2012). In particular, the data include the daily MSCI stock index return series of the following developed countries: Australia, Canada, France, Germany, Italy, Japan, The Netherlands, Spain, United Kingdom, United States, Sweden, Belgium, Norway and Switzerland. We compute the excess log returns for each index using as the benchmark rate r b the world MSCI log return. Hence we obtain 6312 daily log returns from 4 January 1988 to 15 March 2012 for 14 country stock indexes and adjust them by the corresponding world MSCI benchmark rate r b .

Table 1 reports the values on an annual basis for the maximum likelihood estimates of stable Paretian parameters and the basic statistics of individual asset return series: mean, standard deviation, skewness and kurtosis. As a matter of fact, the Central Limit Theorem for normalized sums of independent and identically distributed random variables determines the domain of attraction of each stable law S α (β, σ, δ), which depends on four parameters: the index of stability α∈(0, 2], the asymmetry parameter β∈[−1, 1], the dispersion parameter σ>0 and the location parameter δ (where α=2 corresponds to the Gaussian law). These parameter estimates suggest the presence of heavy tails (since the kurtosis exceeds three and the stability parameter α is less than two) and of skewness (since the asymmetry parameter β and the skewness are different from zero). To test whether asset returns follow a normal distribution, we compute the Jarque-Bera statistic with a 95 per cent confidence level. Similarly, we employ the Kolmogorov-Smirnov statistic with a 95 per cent confidence level to test whether asset returns follow a stable Paretian distribution. Based on these tests, we find that the stable Paretian distributional hypothesis is rejected for 13 countries, the exception being the Swedish country index.

Table 1 Statistics of the asset returns on an annual basis: mean, standard deviation, skewness, kurtosis and Maximum Likelihood Estimates of the stable Paretian parameters (α,β,σ,δ)
Full size table

Even from these preliminary tests, it is reasonable to conclude that the assumption of independent and identically distributed returns and conditional homoskedasticity is not the best model to approximate the return evolution of the country stock indexes investigated in this study. Since the observed market prices involve information on past market movements, we should consider the return distribution conditional on information contained in past return data, or a more general information set. Moreover, in order to properly estimate the measures of risk and reward CoETL and Co-Expected tail profit, we need a large number of observations or simulated data.

GENERATION OF SCENARIOS CONSISTENT WITH EMPIRICAL EVIDENCE

In this section we deal with the problem of scenario generation that is consistent with the empirical evidence. In order to evaluate a robust estimator of a ‘tail’ portfolio measure, we need a sufficient number of observations where the portfolio return is in the tail. In particular, to evaluate the Co-Rachev ratio we require that all the assets are jointly in the tail. Of course, it is difficult to satisfy this condition because by definition these occurrences are very rare events. Thus, even if we have a sample with 6312 daily historical observations, we need to generate a much larger sample of scenarios to propose a robust estimator for the Co-Rachev ratio. Several problems need to be overcome in order to forecast, control and model portfolios in volatile markets. First, as noted in the first section, it is necessary to take into consideration the dependence structure of returns. Second, the portfolio selection problem should be based on scenarios that take into account heavy-tailed distributions, volatility clustering and non-Gaussian copula dependence. Finally, the generation of future scenarios should take into account all the anomalies observed in equity returns, the time evolution and the comovements of the vector of the returns considering the skewness and kurtosis of the joint distribution.

To deal with these problems, we employ a skewed copula with heavy tails. A copula function C associated to random vector υ=(υ1, …, υ n ) is a probability distribution function on the n-dimensional hypercube, such that:

where is the marginal distribution of the ith component (see Sklar, 1959). So once we have generated scenarios with the copula

where is the inverse cumulative function of the ith marginal derived from the multivariate distributional assumption F υ that summarizes the dependence structure of returns, then we can easily generate joint observations using the most opportune inverse distribution functions of the single components applied to the points generated by the copula.

In particular, we next tackle the general problem of return generation considering a multivariate skewed Student’s t copula for the joint generation of innovations of the 14 country index returns. Thus, starting from 1 June 2007, we use a moving window of 5062 daily historical return observations to evaluate the model’s parameters. We generate the scenarios daily and then use the other data from 1 June 2007 to 15 March 2012 for the ex-post analysis.Footnote 2 The period of ex-post analysis has been chosen to include most of the recent financial crises.

The algorithm to generate future scenarios is similar to that proposed by Biglova et al (2009a) and is explained in the appendix. Here we summarize the algorithm we propose to generate return scenarios according to the empirical evidence. We first approximate each return rj, t with an ARMA(1, 1)-GARCH(1, 1) process with stable Paretian innovations and then provide the marginal distributions for standardized innovations of each return used to simulate the next-period returns. Then we estimate the dependence structure of the vector of standardized innovations with a skewed Student t distribution. In particular, we first estimate the dependence structure among the innovations with an asymmetric t-copula. Then we combine the marginal distributions and the scenarios for the copula into scenarios for the vector of future standardized innovations. By doing so, we generate the vector of the standardized innovation assuming that the marginal distributions are α j –stable distributions and that the dependence structure is summarized by an asymmetric t-copula. This procedure allows us to generate future return scenarios using estimated parameters of the ARMA-GARCH model and future scenarios for the model’s innovations.

AN EX-POST EMPIRICAL COMPARISON

In this section, we provide an empirical analysis comparing the ex-post portfolio wealth obtained by maximizing different portfolio performance measures. In particular, for every trading day covering the time period between 1 June 2007 and 15 March 2012 we use a moving window of 5062 daily historical return to evaluate the model’s parameters and then generate 30 000 return scenarios for each portfolio component. We solve a portfolio optimization problem daily based on these generated scenarios. Then we compare the ex-post wealth and total return obtained by maximizing daily a reward-risk performance measure among those proposed in section ‘Performance measures in the presence of systemic risk’: Sharpe ratio as given by equation (2), Rachev ratio as given by (3), and Co-Rachev ratio as given by equation (6). Together with the ex-post results of these portfolio strategies we consider the evolution of the world MSCI index and the wealth we obtain by using a naive strategy of investing an equal amount in each country stock index.

The number of scenarios for which a single return is less than its α percentile is proportional to α. Clearly, the number of scenarios for which all the returns jointly are less than their α percentile is much lower than the previous one and it is not directly proportional to α. Therefore, in order to obtain a robust estimator for the Co-Rachev performance measure, we assume α and β large enough to guarantee that there exist some distressed generated scenarios (that is, such that r1⩽−VaR α (r1), …, r n ⩽−VaR α (r n )). For this reason, we use the parameters α=β=10 per cent for the Rachev and Co-Rachev performance measures. Therefore, for any reward-risk criterion measure ρ(x′r), we can compute the optimal portfolio as the solution to the following optimization problem:

Since we assume that investors invest their wealth in the market portfolio (solution to equation (7)), we consider the sample path of the final wealth and of the cumulative return obtained by maximizing the different performance measures.

Here we summarize the ex-post empirical comparison. According to the algorithm proposed in section ‘Empirical evidence’, every trading day (for a total of 1250 trading days) we generate the future scenarios of the vector of returns. Then, we compare the efficiency of alternative performance measures. We assume that the investor has an initial wealth W0 equal to 1 and an initial cumulative return CR0 equal to 0 (at the date 1 June 2007 ). At the kth recalibration (k=0, 1, 2, …, 1249), the following three steps are performed to compute the ex-post final wealth and cumulative return:

Step 1 Choose a performance ratio. Generate scenarios using the algorithm described in section ‘Empirical evidence’. Determine the market portfolio x M (k+1) that maximizes the performance ratio ρ(.) and is the solution to the optimization problem (7).

Step 2 Calculate the ex-post final wealth as follows:

where rk +1 is the ex-post vector of the returns between k and k+1. The ex-post cumulative return is given by:

Step 3 The optimal portfolio x M (k+1) is the new starting point for the (k+1)th optimization problem (7).

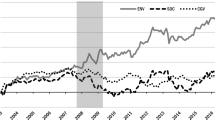
Steps 1, 2 and 3 are repeated for all the performance ratios. The results of this analysis are shown in Figures 1, 2 and 3. Figure 1 shows the ex-post final wealth obtained with the Rachev ratio and the Sharpe ratio. Although the Rachev ratio outperforms the Sharpe ratio, both performance measures are not able to account for the systemic risk during the crisis period. Figures 2 and 3 report the ex-post final wealth and total return obtained by maximizing the Co-Rachev ratio, the Sharpe ratio, and by using a naive strategy of investing an equal amount in each country stock index (that is, 1/14th allocation to each). Also shown in these two figures is the wealth and total return of the world MSCI index. We observe that all the portfolio selection strategies give much better performance (in terms of final wealth and total return) than the world MSCI index. However, only the Co-Rachev ratio appears to be able to account for the systemic risk and the selection strategy based on this measure creates the highest final wealth and total return.

Figure 1
figure 1

Ex-post comparison of the final wealth processes obtained maximizing either the Sharpe ratio or the Rachev ratio.

Full size image
Figure 2
figure 2

Ex-post comparison of the final wealth processes obtained or investing in the MSCI world index or in the equally weighted portfolio or maximizing different reward/risk performances: Sharpe, Co-Rachev.

Full size image
Figure 3
figure 3

Ex-post comparison of the total return processes obtained or investing in the MSCI world index or in the equally weighted portfolio or maximizing different reward/risk performances: Sharpe, Co-Rachev.

Full size image

In order to evaluate the diversification and the turnover of the different strategies, we report in Table 2 both the average of the optimal portfolio weights measured over the backtesting period and we report also the ex-post wealth obtained by the individual country stock indexes during the ex-post period of analysis. A fair conclusion from the results reported in Table 2 is that the strategy using the Co-Rachev performance measure is more diversified than using the Rachev ratio or the Sharpe ratio. As a matter of fact, using either of these two ratios results in an allocation that is (on average) less than 1 per cent in five country stock indexes (France, Italy, the United Kingdom, Sweden and Belgium). Using the Co-Rachev ratio in the selection strategy results in an allocation that is less than 1 per cent to only the United Kingdom and The Netherlands equity markets. Moreover, all three performance measures suggest investing more than 10 per cent (on average) in four country indexes. These countries are the same for the Sharpe and Rachev ratios (the United States, Germany, Australia and Switzerland) but different for the Co-Rachev performance measure (the United States, Japan, Australia and Sweden). Observe that US, Germany, Australia, Sweden and Switzerland indexes always show a positive return on average (see Table 1). The Swedish expected return is the largest and the Japanese expected return is negative and the smallest. Thus, from a simple analysis of the average returns we are not able to justify the success of the Co-Rachev ratio. For this reason, we provide in Table 3 the correlation matrix between the log returns of countries indexes during the ex-post period. Analyzing the correlation matrix, we observe that all of the European index returns are strongly correlated, with the correlation exceeding 70 per cent, while US and Japanese index returns exhibit the lowest correlation (0.12 per cent). Moreover, the Japanese index return has a correlation that is less than 26 per cent with all assets except with the Australian index return (57.74 per cent). Therefore, we conclude that the Co-Rachev ratio provides more portfolio diversification among the returns less correlated (US and Japanese indexes, in particular).

Table 2 Average of optimal weights obtained maximizing different reward/risk performance measures: Sharpe, Rachev and Co-Rachev
Full size table
Table 3 Correlation matrix of the indexes log returns valued on the ex-post period (June 2007–March 2012)
Full size table

Moreover, for all performance measures proposed when used in portfolio selection strategies result in an allocation of about one third (on average) of the wealth in the US stock index, probably because this stock index (together with Canada stock index) presents lower losses during the ex-post period of analysis (see Table 2).

In the last row of Table 2 we report a measure of the portfolio turnover for all portfolio selection strategies. The turnover measure is the average change in the optimal portfolio’s weights over time. That is,

where the vector x M (0)=[xM, 1(0), …, xM, 14(0)]′ is a vector with all the components equal to zero. This measure belongs to the interval [0, 2], where a value of 0 means that the portfolio composition has never been changed during the ex-post period of analysis, while a value of 2 corresponds to the case in which the portfolio would be re-structured completely every day of the ex-post period.

As can be seen from Table 2, portfolio optimization strategies based on the maximization of Co-Rachev ratio is characterized by relatively high turnover, meaning high changes in the portfolio’s weights. In fact, the turnover when using the Co-Rachev ratio is around 1. Thus the portfolio composition change (on average) is around 50 per cent at any recalibration. This result holds because the portfolio composition of the Co-Rachev portfolio strategy often changes completely, which is different from the other portfolio strategies (Sharpe and Rachev) whose portfolio composition remains almost constant for long periods. Therefore, it seems that the observed turnover represents the principal reason for the observed ex-post results. However, a higher turnover adversely impacts portfolio return because of transaction costs. Clearly, transaction costs can be partially reduced utilizing the appropriate exchange traded funds of the country indexes. However, it is still important to evaluate the impact of some transaction costs. For this reason, we have recomputed the ex-post wealth and the total return for all the strategies considering proportional transaction costs.Footnote 3 In order to stress test the impact of transaction costs, we adopt 5 basis points as proportional transaction costs.Footnote 4 In Table 4 we report the values of the final wealth and total return with and without considering transaction costs. We also consider the Sharpe ratio, the Rachev ratio (α=β=10 per cent) of the ex-post return obtained from each portfolio selection strategy.

Table 4 Total return and final wealth, obtained maximizing different reward/risk performances (Sharpe, Rachev, Co-Rachev, Equally weighted) with and without transaction costs
Full size table

We observe that the Sharpe, the Rachev and the Co-Rachev portfolio strategies with and without transaction costs perform better than the equally weighted one. Moreover, the ex-post final wealth (1.1723) and total return (0.14105) of the Co-Rachev portfolio strategy with transaction costs and without transaction costs (1.7998 and 0.64502) are always higher than those observed with the other strategies that always lose wealth during this ex-post period. This ex-post supremacy is also confirmed by the values of the Sharpe ratio and Rachev ratio performances computed on the ex-post returns obtained for the different strategies. These performance values indicate that the Co-Rachev portfolio strategy provides the best ex-post performance with and without considering transaction costs. Moreover, even the strategy based on the maximization of the Rachev ratio shows good performance.

On the one hand, the impact of the transaction costs appears much more evident for the strategy based on the Co-Rachev ratio that still presents the highest final wealth and total return levels. On the other hand, we observe that although by incorporating the transaction costs into the optimization problem the portfolio turnover effect is reduced, it remains the highest for the Co-Rachev ratio. Thus, our empirical analysis strongly suggests that the new performance measure used in a portfolio selection context is able to substantially alter the optimal portfolio composition during a period of global financial instability.

CONCLUSIONS

In this article we discuss the use of different reward-risk performance measures in the presence of systemic risk. First, we propose a reward-risk performance measure that considers the comovement of returns for financial assets. Then we suggest estimating this proposed measure by simulating a sufficiently large number of realistic scenarios. Finally, we apply the proposed performance measure to portfolio selection where the candidate assets are 14 of the country stock indexes included in the global MSCI Barra equity indexes.

The empirical analysis shows that the new reward-risk measure offers the opportunity to generate better performance than other portfolio selection strategies even during periods of financial instability. The use of the new performance measure in portfolio selection problems is characterized by a relatively high portfolio turnover, meaning high transaction costs caused by frequent portfolio re-structuring. However, the new performance measure takes into account the systemic risk and this is the main reason for the superior performance in selecting portfolios with and without considering proportional transaction costs.