Option pricing with a dynamic fat-tailed model

Abstract

In the aftermath of the 2008 financial crisis, the need to consider more realistic risk models for derivative products has received renewed attention. We introduce a dynamic model for the pricing of European-style options with various attractive features such as a mixture of heavy-tails and Gaussian distribution along with a leverage effect property. We test the model on FTSE 100 stock index options during the period of January 2008 to June 2009. Our empirical results show that the model adequately fits the volatility smile dynamics particularly during stress periods. Furthermore, we find that the leverage effect form is driven by the sticky-strike rule.

INTRODUCTION

Financial markets have been subject to stress periods throughout their history. The market stress, which had peaked during the 1987 crash, reaches record levels since the fall of 2008. This raises the question of whether option pricing models have the ability to derive fair contract prices and risk measures in taking such potential stress conditions into account. So far, the financial literature on option theory has documented many well-known pervasive features that affect pricing and hedging while they are not taken into account in the classic Gaussian Black–Scholes–Merton framework (Black and Scholes, 1973 and Merton, 1973).

In order to remedy the assumption of a Gaussian marginal distribution for the underlying asset returns in the classical Black–Scholes–Merton model, three classical approaches are proposed in the literature such as stochastic volatility models,¹ stochastic volatility with a jump-diffusion process for the price² or more general non-Gaussian alternative classes for the underlying asset.³

Nevertheless, volatility smile-consistent option pricing models have reversed the classical approach by using the volatility smile as an input for pricing options.⁴

Derman (1999) popularized two rules of thumbs well-known among professionals who use them to manage the smile dynamics. First, the sticky delta rule (or sticky-moneyness rule) models the volatility as remaining constant to a given moneyness whatever the underlying asset moves up or down instantaneously. Second, the sticky strike rule (or fixed strike rule) models the volatility as remaining constant to a given strike whatever the underlying asset moves up or down instantaneously. The sticky strike rule has the particularity to describe a specific form of the so-called leverage effect. The leverage effect characterizes a surge in the volatility subsequent to a drop in the stock price. Ciliberti et al (2009) show that the stricky strike rule is exact for small maturities while the sticky delta rule becomes more accurate at large maturities.

Surprisingly, there are few studies (Hagan et al, 2002; Daglish et al, 2007 and Ciliberti et al, 2009) using these rules for option pricing. The first motivation of this article is to complete this vacuum. Indeed, the sticky strike rule appears to describe pretty well the dynamics of the leverage effect affecting the volatility smile. However, most of the theoretical models (stochastic and local volatility models) are, in a paradoxal way, not able to take into account this leverage effect dynamics particularly during stress periods; this explains why they produced, during the 2007–2008 financial crisis, huge biases in the risk measures of credit derivative products. The second motivation is to set up a dynamic tractable model, called Hybrid, with a non-Gaussian novel distribution. Notice that the vast majority of existing models are based on a static distribution. The third motivation is to validate empirically the Hybrid model while most of the option pricing models have not been tested empirically particularly during stress periods. Therefore, the model can be used to price options during distressed periods.

The main contributions are theoretical and empirical: first, a dynamic hybrid distribution with heavy tails whose dynamics allows for leverage effect while respecting the non-arbitrage rule; second, a non-Gaussian European-style option pricing model along with an explicit non-Gaussian volatility smile formula; third, an empirical test on FTSE 100 European option contracts from January 2008 to June 2009 with an extensive out-of-sample estimation of the Hybrid model on the overall volatility smile; fourth, an empirical proof that (i) the simple sticky strike rule seems to be adapted for short maturities and (ii) the hybrid distribution can be reduced to an exponential tail in the left part and a Gaussian tail in the right part for most cases.

The article is organized as follows: the next section displays the characteristics of the novel model. The subsequent section exposes the empirical results. The last section summarizes and concludes.

A NEW APPROACH TO NON-GAUSSIAN EUROPEAN OPTION PRICING

The hybrid distribution for the underlying asset price

The static model

This new hybrid distribution is a combination of two fat tails and a central section from a Gaussian distribution. The solution of modelling the extremities with the truncated General Pareto distribution (GPD) is preferred because first, the density remains explicit; second, it allows to connect easily in a continuous way the Gaussian part to the power law tails; third, the continuous constraints between parts allow interesting time scaling rules close to empirical data (see Appendix section ‘The hybrid distribution’). The aim of the Hybrid model is to treat the intermediate case between the truncated Student distribution, which fits empirical returns on a short time horizon of about 10–20 min, and the Gaussian distribution to which the empirical distribution is expected to converge over longer time horizons. Therefore, the Hybrid model should be adapted for an intermediate time horizon around 1 day to several months. This three-part model connected in a continuous way allows pushing the GPD parts progressively to the extremities while the time horizon grows so that the hybrid distribution is converging towards the Gaussian distribution.

The parameters

Six parameters are needed to determine the hybrid distribution, but only two main parameters need to be adjusted daily to market variations (see Appendix section ‘The six free parameters of the model’); indeed, the other four parameters are adjusted with empirical time scaling rules.

The scale parameter Ξ is derived from the standard deviation of the Gaussian part normalized with the square root of the horizon. This parameter mainly moves up or down the smile.

The asymmetry parameter Ω represents the translation from the Gaussian part to its centred position. It is divided by its standard deviation. This parameter describes the asymmetry of the distribution and therefore, the smile asymmetry. It affects the slope of the smile and moves it up or down.

The Γ _L parameter is derived from the distance between the left GPD and the centre of the Gaussian part normalized with its standard deviation. This parameter describes the importance of the Gaussian distribution in the left part of the hybrid distribution; it determines the strike where the smile curvature is enhanced. The greater the parameter, the closer the hybrid distribution is to the Gaussian distribution for Ω=0. By symmetry, Γ _R is derived from the distance between the right GPD and the centre of the Gaussian part. Owing to the asymmetry, this parameter behaves very differently from Γ _L as it diverges relatively quickly and therefore, the right tail is expelled to more than three standard deviations. As a consequence, it does not appear on the smile for a time horizon that is not too short.

The tail index ξ is considered as invariant; its empirical value is often between 1/4 and 1/3 so that the kurtosis may not be defined without any tail cut-off. This parameter impacts the smile curvature with the condition that the Gaussian part (Γ _L , Γ _R ) is not too heavy.

The Θ _L parameter is derived from the ratio of the left tail cut-off, denoted δ _L cut, over the scale parameter β _L of the left GPD. This parameter describes the strength of the truncature given that the more δ _L cut is weak, the more the truncature is strong. Θ _L , Γ _L and ξ mainly impact the curvature of the smile. The Θ _R parameter is less important as the right tail is expelled very quickly. These Θ _L and Θ _R parameters change the curvature along with the up and down direction of the smile.

From these six free parameters, we can deduce Γ _R from Γ _L or Γ _L from Γ _R resolving a non-linear equation to make sure that the expectation of the hybrid distribution is reduced to zero through numerical iterations. This equation (see Appendix section ‘The non-linear equation’) uses the hypothesis that the different parts are connected in such a way that the density and its first derivative are continuous. Empirically, it seems that beyond a horizon of a couple days, the optimal solution corresponds to the case where the right tail is expelled very far away from the higher strikes. In addition, up to a couple of months, the Ω parameter is increasing in absolute value, as the left tail is moving closer to the centre of the Gaussian part while progressively reducing to its exponential shape. After a couple of months, the Ω parameter starts to converge slowly to zero and the Γ _L starts to diverge. The two main parameters Ξ and Ω are adjusted daily for each maturity. The remaining four parameters follow a time scaling rules to calibrate the Hybrid model over relative short horizons where extreme strikes exist:

• ξ is invariant.

• Θ _L is decreasing as a power of ξ.

• Θ _R is decreasing as a power of ξ.

• Γ _R is increasing as a power of 1/2.

The dynamic model

The option pricing standard approach generally consists in determining a theoretical process generating a distribution along with an associate volatility smile. The drawback is that such a distribution does not well reproduce the volatility smile dynamics (for example Bergomi, 2004, 2005). For this reason, we choose the inverse approach that consists in determining an empirical distribution and validating econometrically its dynamics from the market prices (see Appendix section ‘The distribution dynamic model’). The drawback is that it is difficult to recover the exact process that reproduces this distribution along with its dynamics. As a consequence, the non-arbitrage constraint (see equation (A.9)) that controls for the parameter values relative to the underlying asset variations is approximately matched.

Concretely speaking, we suppose that the distribution of the parameters is not invariant whatever the variation of the underlying asset. Indeed, this allows the distribution to capture the smile dynamics. The most realist way to model the dynamics is to allow a little variation of the parameters when the underlying price varies. The dynamics of implied volatilities is then derived assuming that only the Ξ and Ω parameters are changing after an instantaneous variation of the underlying price (see equations (A.12a) and (A.12b)), that is, Γ _R , ξ, Θ _R and Θ _L are not sensitive to the instantaneous variation of the underlying price.

The hybrid option valuation model

The Hybrid model uses risk-neutral valuation approach. The link between the real and the risk-neutral probabilities is assumed to remain valid even if the method is applied to a non-Gaussian distribution. The centred logarithmic equity returns x at the time horizon τ are assumed to follow, under the risk-neutral probabilities Q, the hybrid distribution (see Appendix section ‘The option pricing notations’). The valuation of European puts and calls with a strike price K and a maturity τ starts first with the risk-neutral formula from the Black–Scholes–Merton setup (Black and Scholes, 1973 and Merton, 1973) and second with integration by parts and change of variables methods. We obtain three different regimes depending if the strike price is close to the money, high and far from the money or small and far from the money (see Appendix section ‘The option pricing formulae’). The most general formula for the call options is equation (A.16). The call-put parity gives the corresponding put price.

Note that these formulae are not completely explicit. Indeed, it is necessary to solve first the non-linear equation in order to determine Γ _R from Γ _L or Γ _L from Γ _R so that we make sure that the expectation of the hybrid distribution is equal to zero. In addition, it is possible to determine, thanks to perturbations calculus, the at-the-money (ATM) volatility, the ATM smile’s slope, the ATM smile’s curvature (see Appendix section ‘The skew and the curvature near the money’). The most general formula for the volatility smile is given by equation (A.20).

THE EMPIRICAL RESULTS

The dataset

The dataset⁵ consists in European option contracts on the FTSE 100 stock index. Bid-ask spreads are used in the study for quality measure. The extensive period of observation is from January 2008 to June 2009. It is divided into two parts: first, the period from January 2008 to August 2008 is used to calibrate the dynamics of the model and second, the period from October 2008 to June 2009 is used for the out-of-the sample empirical test. This second time period is critical as it includes the historical crash sub-period of the last quarter of 2008. It allows testing the dynamic model on a financial distressed period. Three types of option contracts are discarded. First, only options with the two shortest maturities are selected because of their high liquidity, with a maximum time horizon of 2 months. We work on every first bid and first ask from 16:00 to 16:04 on every day, at every strike and maturity. The underlying price discounted by the expected dividend yield is estimated thanks to the ATM call-put parity. The risk-free interest rates are the 2 weeks Libor rates. Second, only near-the-money and out-the-money (OTM) prices are used as OTM contracts are more liquid than in-the-money contracts. Third, in order to have only significant option prices, we retain at each strike, the lowest bid-ask spread identified from 16:00 to 16:04. In the same logic, if the lowest volatility spread is greater than 2 × 5 per cent, it is not taken into account but an exception is made when the maturity is lower than 2 days. Indeed, at these very low maturities, the impact of this uncertainty is generally acceptable. Note, that during the distress period of October and November, option contracts are not priced very far from the money; this has enlarged the market spread. Table 1 exhibits data descriptions. It reveals that the most extreme strikes are located at maximum 2.3 standard deviations from the underlying price.

Table 1 Descriptive statistics

The dataset displays volatility smiles characterized by a strong negative slope with a weak curvature (see Figure 1). This strong asymmetry manifests itself as follows. First, the Gaussian central right part repels the right tail distribution up to three standard deviations, which means that the limit separating this Gaussian part and the tail distribution is superior to three times the Gaussian standard deviation (Γ _R >3). Second, the left tail distribution occupies the whole space and maintains the Gaussian part in the central axis (Γ _L ≈0). The weak curvature manifests itself as follows. First, the right tail is already neglected to create the asymmetry. Second, the left cut-off parameter Θ _L is close to zero, which transforms the left tail distribution into its exponential component. In conclusion, the dataset reveals that the hybrid distribution⁶ transforms into a Gaussian right part and an exponential left part. This might be interpreted as a manifestation of risk aversion.

Figure 1

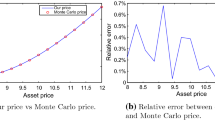
Volatility smile on 17 October 2008.

Figure 1 displays the volatility smile on the 17 October 2008. On the day, the FTSE 100 stock index returns strongly rebounded about at +5.0 per cent as a reaction of one the severe decrease of the 16 October 2008 when the stock index returns reached −5.5 per cent. The in-the-sample smile corresponds to the true smile and serves as a benchmark. Even in this stress context, the Hybrid model is able to move in the right direction and finished closed to the true smile.

The hybrid distribution estimation

First, we calibrate the static hybrid distribution with Visual Basic Package. We consider a three-step minimizing procedure for the distribution model calibration. The first step corresponds to the static model calibration while the second step corresponds to the dynamic model calibration. The procedure allows reducing the problem dimension from six parameters to only two because Ξ and Ω parameters are the remaining time-varying parameters. In-the-sample period is from January 2008 to August 2008.

Step 1: Parameter estimates of Θ _L , Θ _R and Γ _R are denoted, respectively, by Θ* _L , Θ* _R and Γ* _R ; they are calibrated over the whole in-the-sample period and have a 1-day horizon. They will no more be estimated but directly computed for any time period given that they are assumed to follow a specific time scaling rule. ξ is estimated directly on the FTSE 100 stock index for avoiding cumbersome computations. It also follows a specific time scaling rule. Let T denote the number of days in the sample, N _t is the number of contracts traded on date t with τ=T−t; N _t also corresponds to the number of strike prices; let φ be the set of parameters Θ* _L , Θ* _R , Γ* _R . The sum of squared errors in implied volatilities is computed at each date in the form of an Implied Volatility Mean Square Error.

With e_{k, t} representing the difference between the markets mid bid-ask implied volatilities and the theoretical implied volatilities of the kth strike price at date t with k=1, …, N _T . This approach is better than the traditional literature choice of price minimization. Indeed, the level of implied volatilities is homogeneous according to the spectrum of strike prices while it is not the case for options prices. Therefore, the estimation procedure is more stable and reliable.

Step 2: In-the-sample calibration for the time varying Ξ and Ω parameters. They are estimated each day for all strike prices available. A two-step minimization procedure is used to calibrate the Ξ and Ω parameters to the current day’s smile. First, it estimates the correct Ω parameter thanks to the one-dimensional Marquardt minimization. Then, it adjusts the Ξ parameter thanks to the one-dimensional Marquardt minimization. The remaining set of parameters (Θ _L , Θ _R , Γ _R and ξ) is computed given their estimation in Step 1 and their specific time scaling rules.

Step 3: The estimation of the dynamic model is implemented using panel regression procedure with the econometric software Eviews. Equation (A.12a) is estimated first, then equation (A.12b). Let φ _a be the set of parameters , , of equation (A.12a) and φ _b the set of parameters of equation (A.12b) (see Appendix section ‘The distribution dynamic model’).

The out-of-the-sample option valuation procedure

To assess the differences between market volatilities and theoretical volatilities for an out-the-sample fit, we use the Mean Implied Volatilities Forecast Error (MIVFE) to quantify the error magnitude and the component analysis to see the origin of the bias.

With e_{k, t} representing the difference between the markets mid bid-ask implied volatilities and the forecasted implied volatilities of the kth strike price at date t with k=1, …, N _T . Φ and ξ are computed from the in-the-sample calibration; during the out-the-sample procedure, they are adjusted according to the time scaling rules. Ξ and Ω are computed from the in-the-sample calibration; during the out-the-sample procedure, they are adjusted for the underlying price variations dp using the in-the-sample dynamic model. dp remains the only input stemming from the out-the-sample period.

The out-of-the-sample hybrid option model performance

Table 1 presents descriptive statistics of the daily European option contracts on the FTSE 100 stock index. The dataset is divided into two periods: the first one corresponds to the in-the-sample period from January 2008 to August 2008; the second one corresponds to the out-the-sample period from October 2008 to June 2009. We note unsurprisingly that the average daily bid-ask spreads are highest during October 2008, which is with October 1987, the months with the highest volatility since World War II. The average daily ATM volatility and the standard deviation of this ATM volatility confirm the volatility peak in October 2008. The average maximum moneyness shows, for example, that during October 2008, the strike prices were at 1.5 standard deviations from the underlying prices. Figure 1 displays the volatility smile on 17 October 2008. On that particular day, the FTSE 100 stock index strongly rebounded by +5.0 per cent as a reaction to a severe decrease on 16 October 2008 when the stock index declined by −5.5 per cent; this kind of fluctuation strongly affects the smile dynamics. But, even in this stress period, the Hybrid model is able to move in the correct direction and finishes close to the true smile.

Table 2 presents the estimation of the six free parameters characterizing the hybrid distribution along with the empirical dynamic model. The Ξ and the Ω parameters are estimated on a daily basis. The four other parameters are estimated during the in-the-sample procedure and re-computed on the time scaling rule basis as explained in the section ‘The hybrid distribution estimation’ (Figure 2).

Table 2 Parameter estimations

Figure 2

One-day ahead pricing performance error analysis.

Figure 2 displays the one-day ahead pricing performance error analysis for the Hybrid model. This graph corresponds to Table 6. The error decomposition reveals that the translation error explains most of the short-term errors in the smile dynamics.

Table 3 presents one-day ahead (out-the-sample) average pricing performance of the Hybrid model. As a benchmark, we choose a practitioner form of the Black–Scholes model (1973) that we call sticky strike model in reference to the Derman’s (1999) model where the volatility smile has no dependence to the index level S₀ and varies only with the strike price K and the time to maturity τ. We choose this heuristic model because it offers an absolute zero-cost computing effort with a relative very good out-the sample pricing performance. However, its performance should decline with long maturities. An in-the-sample procedure estimation of the sticky strike model yields the computation of the true implied volatility. In addition for this table, we add as a standard benchmark, the Black and Scholes (1973) model, where the previous day’s implied volatility is used to compute today’s option price. Finally, as a supplementary comparison, we reproduce the out-the-sample pricing error proportion between the stochastic volatility models (SV, SVSI, SVJ) of the Bakshi et al (1997) article and the reported Black and Scholes (1973) model. We conclude that the Hybrid model has a relatively good out-the-sample pricing performance with the exception of October 2008 month when the volatility reaches its highest level; in average, over the whole out-the-sample period, the pricing error is 2.37 per cent for the Hybrid model against 2.27 per cent for the sticky strike model; for the Black and Scholes (1973) model, the pricing error is about 6.7 per cent and in proportion, it is around 5.4 per cent for the stochastic volatility models. Figure 3 displays the implied volatility error function of the Hybrid model and the sticky strike model. The errors appear to be highest for short maturities and remain below 5 per cent for medium and long maturities; the Hybrid model behaves here like the sticky strike model.

Table 3 One-day ahead pricing average performance

Figure 3

Hybrid model and sticky strike model implied volatility error.

Figure 3 displays Hybrid model and sticky strike model’s implied volatility error. Implied volatility error is computed as the difference between a theoretical implied volatility and a market implied volatility. The difference between the Hybrid model’s implied volatility and the true implied volatility is shown to be the highest for short maturities and to be below 5 per cent for medium and long maturities.

Table 4 presents one-day ahead pricing performance per range of moneyness for the Hybrid model and the sticky strike model. Small strikes, medium strikes or high strikes are defined relatively to moneyness in contrast with many studies where an arbitrary threshold is set. The error magnitude of the Hybrid model seems globally stable and it performs at least as better than the sticky strike model for medium and high strikes.

Table 4 One-day ahead pricing performance per range of moneyness

Table 5 presents one-day to five-days ahead (out-the-sample) pricing performance for the Hybrid model and the sticky strike model. The out-the-sample pricing performance of the Hybrid model remains comparable in magnitude with the sticky strike model with an average relative error that is increasing with time by an average factor of 0.6 per cent per day.

Table 5 One-day to five-days ahead pricing performance

Table 6 presents one-day ahead pricing performance error analysis for the Hybrid model and the sticky strike model. We note that the Hybrid model has globally negative errors with a relative low magnitude. Nevertheless, the error decomposition reveals a nice stylized fact as most of the short-term errors for the smile dynamics is caused by a translation error for both models. In addition, this translation error is jumping to 4.4 per cent for the Hybrid model against 3.5 per cent for the sticky strike model during the most volatile month of the financial crisis, that is, October 2008. Figure 2 displays this remarkable fact. These translation errors explain why the errors are homogeneous for all strikes as it is shown in Table 4.

Table 6 One-day ahead pricing performance error analysis

CONCLUSION

This article brings new insights about non-Gaussian volatility smile dynamics. We derive a novel European-style option pricing model and implement it on the FTSE 100 stock index from January 2008 to June 2009.

The theoretical contribution of the article is to derive a non-Gaussian European-style option pricing model with the following features:

• A static hybrid distribution with three components: two GPDs for the tails and one Gaussian distribution in the centre.

• A dynamic hybrid distribution controlled by six parameters: four parameters follow a simple time scaling rule and two parameters follow an empirical dynamic model able to capture the leverage effect.

• An explicit non-Gaussian volatility smile formula where the smile asymmetry is completely explained by the leverage effect.

The empirical contributions of the article are twofold:

First, according to the in-the-sample calibration:

• The hybrid distribution can be reduced to an exponential tail in the left part and a Gaussian tail in the right part for maturities going from 1 day to 3 months; this explains why the Hybrid model captures the type of volatility smiles with strong asymmetry but weak curvature.

• The empirical dynamic model parameters are closed to the sticky strike rule, which empirically proves that this rule fits well short maturity option contracts.Second, according to the out-the-sample test:

• The Hybrid option model pricing performance is almost three times better than the Black and Scholes (1973) model and remains comparable to the sticky-strike model.

• A big proportion of the pricing errors stems from the short-term contracts and are mainly explained by a simple translation error of the volatility smile; in addition, the remaining errors have the same magnitude of the bid-ask spread.

This work can be extended to risk management measures such as VaR but also to derivative contracts such as credit default swap.

Appendix

The parameters of the distribution

The six free parameters of the model

The hybrid distribution is determined by six free parameters used for the model calibration:

• The scaling parameter ; adjusted for each maturity.

• The asymmetry parameter Ω=−(μ/σ); adjusted for each maturity.

• The right (left) Gaussian part length parameter Γ _R =((δ _R −μ)/(σ)) (Γ _L =(δ _L +μ)/(σ)) increases as a power of (1/2); the Gaussian part length parameter Γ=Γ _L +Γ _R .

• The tail index parameter ξ is invariant.

• The left cut-off parameter Θ _L =(δ _Lcut /β _L ); decreasing as a power of ξ.

• The right cut-off parameter Θ _R =(δ _Rcut /β _R ); decreasing as a power of ξ.

These six free parameters are based on the characteristic parameters of the distribution (see Appendix section ‘The hybrid distribution’). There are sufficient to determine the hybrid distribution, thanks to the non-linear equation (see Appendix section ‘The non-linear equation’).

The non-linear equation

The non-linear equation is:

This equation (A.1) allows to:

• Link the Γ _R parameter to the Γ _L parameter.

• Deduce σ, μ, δ _R , δ _L , δ _Rcut , δ _Lcut , β _R , β _L , ξ from Ξ, Ω, Γ _L (or Γ _R ), Θ _L , Θ _R and ξ.

The equation (A.1) uses two well-known Γ and N integrals deriving from the Incomplete gamma function and from the Gauss error function defined as:

• Γ(a, x)=∫ _x ^∞ e ^−t t ^a−1 dt is finite if x>0.

• .

The equation is a direct result from the five following conditions:

• 1 The mean of the hybrid distribution must be null.

• 2 The Pareto and the Gaussian left parts must be linked so that the density is continuous.

• 3 The Pareto and the Gaussian left parts must be linked so that the first derivative of the density is continuous.

• 4 The Pareto and the Gaussian right parts must be linked so that the density is continuous.

• 5 The Pareto and the Gaussian right parts must be linked so that the first derivative of the density is continuous.

Solving this equation is needed in order to compute the density of the hybrid distribution (see appendix section ‘The hybrid distribution’) and to price options (see section Appendix ‘The option pricing notations’). It is solved numerically by iteration. More precisely, it allows determining Γ _L from Γ _R along with the others parameters of the hybrid distribution; solving this equation is similar to find the function L so that Γ _L =L(Γ _R , Ω, …). The function L is not defined everywhere as the equation has not always a solution; the function L is defined for a determined interval.⁷

Once the equation is solved, it is easy to determine σ, μ, δ _R , δ _L , δ _Rcut , δ _Lcut , β _R , β _L , ξ from the six free parameters Ξ, Ω, Γ _L (or Γ _R ), Θ _L , Θ _R , ξ along with τ:

The hybrid distribution

The hybrid distribution is used to model the centred logarithmic returns x of the underlying prices at a specific time horizon τ under the risk-neutral probabilities Q. Its density ρ(x) is modeled in three parts as three different functions of x connected in a continuous way for both the density and its first derivative:

• 1 If x<−δ _L , x in absolute value is greater than the left threshold parameter, and the density is then derived from the left exponentially truncated GPD shifted by the left threshold parameter, resulting in:

  

• 2 If −δ _L <x<δ _R , x in absolute value is smaller than the left and right threshold parameters, and the density is then derived from the Gaussian distribution shifted by the center parameter, resulting in:

  

• 3 If x>δ _R , x in absolute value is greater than the right threshold parameter, and the density is then derived from the right exponentially truncated GPD shifted by the right threshold parameter, resulting in:

  

where the different parameters are defined as follows:

• The tail index parameter ξ.

• The scale parameter of the right (left) tail β _R (β _L ).

• The cut-off parameter of the right (left) tail δ _Rcut (δ _Lcut ).

• The threshold parameter of the right (left) δ _R (δ _L ). This parameter defines, in the hybrid distribution, the limit between the Gaussian section and the truncated GPD of the right (left) side.

The distribution dynamic model

The link between the volatility smile’s dynamics, the Hybrid model and no-arbitrage rule

The smile’s dynamics must obey to a condition in order to avoid any arbitrage opportunities. For example, if a portfolio is built up with a long position on a call option with strike K₁, a short position on call option with strike K₂ not too far from K₁ and a delta hedging with futures contracts; this portfolio must gain, in average, the risk-free rate. This condition can be:

Owing to the no-arbitrage rule, this relation should not depend any more on the strike K. The smile response (∂σ _i (K, f))/(∂f) (the implied volatility σ _i is depending on the strike K and the underlying asset f) to a small change in the futures⁸ price ∂f mainly depends on its initial shape and on the six free parameters. If the parameters remain constant, the smile response will only do a translation and depends only on its initial shape. In reality, two parameters, Ξ and Ω are sensitive to the underlying price variation. Therefore the smile response will also depend on the scale parameter’s response (∂Ξ)/(∂f) and on the asymmetry parameter’s response (∂Ω)/(∂f). The other parameters Γ _L , Θ _L , Θ _R and ξ are supposed to remain constant after a futures price variation. The volatility smile’s dynamics is therefore given by:

If we only retain the two first terms and the two last terms by neglecting the other terms of higher order, the smile’s dynamics is reduced to two dimensions ((∂²Ξ)/(∂f²), (∂²Ω)/(∂f²)):

However, it is difficult to deal with the scaling parameter Ξ when other parameters are changing. Indeed, the standard deviation of the hybrid distribution depends on both Ξ and Ω; hence, the smile’s level depends also on these two free parameters. In order to ensure that this standard deviation depends only on the scaling parameter, it must be corrected with a change of variable of Ξ into Ξ _sd . Unfortunately, there is not any simple formula for it. Thanks to a new function denoted F _sd , we finally work with the following new variables:

F _sd is obtained through direct integration:

Fortunately, some approximations can be done by replacing to obtain a simplified formula

Combining equations (A.5), (A.6) and the simplified formula of (A.7) gives:

This result is important as it provides an explicit relation of the smile’s dynamics given the no-arbitrage rule. The combination of equations (A.3) and (A.8) gives equation (A.9). This relation represents a constraint to the two main degrees of freedom (Ω _sd , Ξ _sd ) of the Hybrid model; as they drive the dynamics of the volatility smile, this relation also constrains the smile’s dynamics.

As a consequence, the no-arbitrage rule constrains the smile’s dynamics (∂²σ _i (K, f))/(∂f²).

The empirical dynamic model

Two equations are needed for modelling both the response of Ξ and of Ω to a variation of the underlying futures price. As explained previously, itis better considering the variations of Ξ _sd and Ω _sd rather than the variations of Ξ and of Ω; indeed, Ξ _sd not only corresponds to the standard deviation of the hybrid distribution, but it remains a compatible scale parameter whatever the other parameters Ω _sd , Γ _L (or Γ _R ), Θ _L , Θ _R and ξ are changing or not. More precisely, these other four parameters Γ _R , Θ _L , Θ _R and ξ are supposed to be sensitive only to the elapsed time according to the different power laws introduced in Appendix section ‘The six free parameters of the model’.

For small variations in , the variation of Ξ _sd corresponds to ; all the variables in ε noted hereafter are considered as noises. This relation controls for the volatility smile level but can be interpreted as the leverage effect; indeed, the more the underlying asset decreases, the more the volatility increases. The leverage effect is inversely proportional to , which makes sense as the leverage effect is only transcient. The leverage effect is also proportional to Ω, which corresponds also approximatively to the slope of the smile according to second equation of (A.20). This equation can be interpreted as if the asymmetry of the smile was completely explained by the leverage effect. If is close to unity, the model becomes close to the ‘sticky strike rule’ around-the-money where . In that case, as a consequence of the no-arbitrage rule and some others approximations, a non-linear differential equation is obtained for Ω _sd ; this non-linear equation constrains the empirical dynamic model:

Equation (A.11) is a simplification of equation (A.9).

For larger variations in dp, we add two mean reversion terms. Using panel regression procedure on Eviews, we obtain therefore for the empirical dynamic model the two following stochastic equations:

where , and . Thanks to the no-arbitrage rule, and are linked to by the last differential equation (A.11): . This relation allows the equation (A.12b) to be partly deduced from the equation (A.12a).

We can interpret each term of this dynamic empirical model as follows:

• 1 The first term is a direct result of the leverage effect for small variation.

• 2 The second term is used for larger variation in price and is an indirect result from the leverage effect due to the term in the variation of Ω _sd .

• 3 The third term is a mean reversion term, so that the implied volatility remains not too far and not for a too long time from the real volatility. q is the ratio between the real volatility (estimated with the 5 min frequency returns for the last 24 hours, before 15:00 in our case, when the market is open) and Ξ _sd : . c, a slight correction in order to take into account a scaling effect correction, is estimated around 0.73 for the FTSE.If the discrepancy is null, then q=1 and there is not any correction from the mean reversion. We choose to have a mean reversion effect proportional to (1)/(1+(τ)/(dτ)) in order to have a long memory process. That also allows for the dynamic system to remain valid when changing the time lag. Finally, we observe that the greater is the maturity τ of the option, the smaller is the mean reversion effect; when combined with the leverage effect, this will create a term structure of implied volatilities.

• 4 The fourth term is the first derivative of Ω _sd . It must be consistent with the no-arbitrage rule and the differential equation (A.11); we assume a constant term to simplify.

• 5 The fifth term is twice the second derivative of Ω _sd . It was chosen to be proportional to Ω _sd as an approximate solution of the differential equation obtained from the no-arbitrage rule hypothesis.

• 6 The last term is a mean reversion term so that Ω _sd remains not too far from a power law explained by the leverage effect. If τ<<τ _c , then Ω _sd is moving around a power law decreasing as converging to zero when τ is tending to zero. τ _c corresponds to the maturity where the asymmetry is maximum in absolute value; beyond τ _c , the leverage effect has smaller impact and therefore, the distribution can converge slowly to the Gaussian case without any asymmetry for τ tending towards ∞ as expected.

The option pricing model

The option pricing notations

• By definition of the risk-neutral probabilities, the expected return must gain the riskless interest rate r, with S ₀ being the initial underlying asset price and S _τ the underlying asset price at maturity:

and

The expected logarithmic returns, from equation (A.13b), produce riskless interest rate corrected by the term of 0.5Σ². This correction is necessary to validate the put-call-parity.

with

Let us define now the moneyness α as:

with K being the strike price. As a reminder, log ((S _t )/(S₀))−rτ+(∑²)/(2) is supposed to be distributed according to the hybrid distribution under the risk-neutral probabilities Q. The valuation of European puts and calls with a strike price K and a maturity τ starts first with the risk-neutral formula from the Black–Scholes–Merton setup just below and second with integration by parts and change of variables method.

• γ _R , γ _L , γ _g defined as the weight of the differents parts in the hybrid distribution.

We must first evaluate Σ, γ _R , γ _L , γ _g before computing the option prices. The option pricing model is not based on the six free parameters. This is because of the fact that there are no explicit solutions from the non-linear equation (A.1); therefore, only numerical solutions remain available.

In most cases, we note empirically that Σ tends to σ. The call prices will be finite if the right tail cut-off δ _Rcut remains smaller than unity. Indeed, if δ _Rcut is greater than unity, the call prices depend linearly to the infinite integral Γ(a, x) if the x<0.

The option pricing formulae

We obtain three different regimes depending on the moneyness where the strike price is: (1) high and far from the money, (2) close to the money or (3) small and far from the money:

• 1 Regime 1: Case where strikes are high and the moneyness is greater than the right threshold parameter (that is α>δ _R ); we recall that the threshold parameter δ _R defines the limit between the Gaussian section and the truncated right tail. Therefore, only the right truncated tail of the hybrid distribution is used to obtain the price of the deep out-the-money (OTM) calls. Only two terms are obtained in the formula mainly depending on the initial price, the strike, the right threshold and the right cut-off δ _Rcut parameters but also from the function A(z):

  

  The function denoted A(z) is finite if z is greater than 0. The right tail cut-off δ _Rcut must be smaller than unity so that the call price keeps finite. This function depends on the moneyness but also on the ξ, the right scale β _R , the right threshold parameter δ _R and the right weight γ _R defined as below:

  

  with:

  
  

  γ _R , Σ, σ, δ _Rcut depend on Ξ, Ω, Γ _R , Θ _L , Θ _R , ξThe corresponding deep in-the-money (ITM) put price is a direct result from the call-put parity:

  

  Table 2 reveals that, in average, Γ _R is close to 6; given that Γ _R =(δ _R −μ)/(σ), we can deduce by neglecting μ, that δ _R ≈6 standard deviations; therefore, the case for α>6σ remains only theoretical.

• 2 Regime 2: Case where strikes are close to the money or even at-the-money (ATM); the moneyness in absolute value is smaller than the right and left threshold parameters (that is −δ _L <α<δ _R ); we recall that the threshold parameter δ _L defines the limit between the Gaussian section and the truncated left tail. Table 2 reveals that, in average, Γ _L is close to 1; given that Γ _L =(δ _L +μ)/(σ), we can deduce by neglecting μ, that δ _L ≈1 standard deviation; therefore, the case for −1σ<α<+6σ gives the most general formula for option pricing:

  

  A similar formula to the Regime 1 is obtained but with two other terms derived from the Gaussian part of the hybrid distribution. The function denoted A(z) is slightly different from the Regime 1 (α is replaced by the limit δ _R between the Gaussian part and the right GPD of the hybrid distribution). The function denoted B(z) allows to meet the Black and Scholes (1973) formula if the threshold parameters δ _R and δ _L tend to infinity. In that case, the asymmetry parameter Ω tends to 0 and the Gaussian part weight γ _g tends to 1; the weight of the right GPD γ _R tends to 0:

  

  where:

  
  

  γ _R , γ _g , Σ, σ, δ _Rcut depend on Ξ, Ω, Γ _R , Θ _L , Θ _R , ξThe corresponding put option is also obtained from the call-put parity:

  

• 3 Regime 3: Case where strikes are small and the moneyness in absolute value is greater than the left threshold (that is α<−δ _L ). Therefore, by a symmetrical way, only the left side truncated GPD of the hybrid distribution is used to obtain the price of the deep OTM put. Only two terms are obtained in the formula. The formula is similar to the Regime 1 except that the sign and (1−δ _Rcut )/(δ _Rcut ) are changed, which allows put options to have finite prices even if the cut-off δ _Lcut is greater than unity:

  

  The function denoted A(z) is similar to the Regime 1. Only α is replaced by −α:

  

  with:

  
  

  γ _L , Σ, σ, δ _Lcut depend on Ξ, Ω, Γ _R , Θ _L , Θ _R , ξThe deep ITM call price is a direct result from the call-put parity:

  

The skew and the curvature near the money

The ATM implied volatility, denoted σ _i (K, K), can be approximated using perturbation calculus (i) when the right GPD part is neglected (that is, Γ _R >>1), (ii) when the strike price remains near-the-money in the Regime 2, (iii) and when Ω is negative but not too great in absolute value. This approximation is, in a surprising way, most of the time quite valid except for very short maturity less than a couple of days and for extreme strikes. Moreover, in this situation, we can also have an approximation for the shape of the smile in the neighbourhood of the money with the slope, (∂σ _i (K, K))/(∂K), and the curvature, (∂²σ _i (K, K))/(∂K²). We obtain the following results:

where:

We can check that the left GPD part allows exhibiting an important skew without an excessive curvature near-the-money; that is exactly what happens in the market. Even if the approximations used are not any more justified far from-the-money, the results are useful to see how the shape of the smile is sensitive to the different parameters.⁹