Loans, ordering and shortage costs in start-ups: a dynamic stochastic decision approach

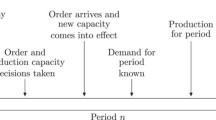
Abstract

Start-up companies are a vital ingredient in the success of a globalised networked world economy. We believe that such companies are interested in maximising the chance of surviving in the long term. We present a Markov decision model to analyse survival probabilities of start-up manufacturing companies. Our model examines the implications of their operating decisions, in particular how their inventory strategy is influenced by purchasing, shortage, transportation and ordering costs, as well as loans to the firm. It is shown that although the start-up company should be more conservative in its component purchasing strategy than if it were a well-established company it should not be too conservative. Nor is its strategy monotone in the amount of capital available.

Appendix

Proof of Lemma 1

The proof is by induction on n. Since q(n, i, x)=0 when x+αCi<0 for all n, q(0, i, x)=1 when x+αCi⩾0 for i⩾0 and q(1, i, x)⩽1 when x+αCi⩾0 and i⩾0, all three hypotheses hold in the case n=0.

Assume all three hypotheses hold for n, and use max _i {a _i }−max _i {b _i }⩽max _i {a _i −b _i } to show for given values of r, w⩾0, and α⩾0 that

Hence, hypothesis (i) holds for n+1.

Hence, hypothesis (ii) holds for n+1.

Hence, hypothesis (iii) holds for n+1.

Proof of Lemma 2

(i) Suppose the optimal action in state (n, i+j, x−jC−w) is k(n, i+j, x−jC−w)=δ⩾0, and consider the particular action that orders j+δ in state (n, i, x). As i⩾M, from Equation (1) we have

as −min(w, (j+δ)w)⩾−w−min(w, δw)∀j, δ, w⩾0, arriving at the desired inequality q(n, i, x)⩾q(n, i+j, x−jC−w).

(ii) It is sufficient to prove property (ii) for j=1, and the proof will be by induction on n. The result is trivially true for n=0 as q(0, i, x)=1 ∀i⩾0 and x+αCi⩾0. Assume that it is true for n−1. Let

and let k(n, i+1, x)=δ be the optimal action in state (n, i+1, x), and consider the action that orders δ in state (n, i, x+S) for i⩾M, or state (n, i, x+S+r) for i<M. We have

where the second inequality follows from the induction hypothesis, and Lemma 1 (ii). This proves the induction hypothesis holds for n, and the result follows.

Proof of Lemma 3

q(n, i, x) is bounded above by 1 and below by 0, and from Lemma 1 (i) is monotonic non-increasing in n. As bounded monotonic sequences converge, point (i) follows. Points (ii) and (iii) follow immediately by taking the limit in the results of Lemma 2, and points (iv) and (v) follow by taking the limit in the results of Lemma 1 parts (ii), (iii).

Proof of Lemma 4

The proof uses the policy iteration algorithm for dynamic programming models (see Puterman⁶). Let us first focus on the parsimonious policy described in Equation (4) for w>0. When this policy is applied, the average reward and bias terms, Equation (2), satisfy the following equation:

It is easy to verify by substitution that the values of g and v(i) in Equations (3) satisfy this equation.

Note that if we describe the two expression for v(i) in Eqs. (3) as v ₁(i) if i⩾M, and v ₂(i) if i<M, then expression v ₁(i)⩾v ₂(i) since

Now apply a policy improvement step to verify that the policy of Equation (4) is optimal.

For states i⩾2M, and w>0 the policy improvement step looks for the action k which maximises

and we wish to show that this occurs when k=0. This would be the case if

Since i−d and i+k−d⩾M the corresponding bias term v(i−d), and v(i+k−d) are in fact v ₁(i−d) and v ₁(i+k−d), so we require Sd−H+C(i−d)+(S−C)d+(i−d)w/N⩾Sd−H+C(i+k−d)+(S−C)d+(i+k−d)w/N. Simplifying we need . Since k<N this inequality holds.

For M⩽i⩽2M, we want to show that

for any k, 0⩽k⩽N. If i+k−d⩾M the corresponding bias term (v function) is v ₁. This means we want

This is trivial as k⩽N. On the other hand, if i+k−d<M, then the right-hand side is v ₂(i+k−d) not v ₁(i+k−d) and since v ₂(i+k−d)⩽v ₁(i+k−d) the inequality still holds.

For i⩽M, we want to show that

This reduces to the previous case since the shortage r, and the sales S terms cancel on both sides and v(i+k−min(i, d)⩽v ₁(i+k−min(i, d)).

Now look at the parsimonious policy for w=0, and i⩽2M. First evaluate the policy described by Equation (5). When the policy is applied, the average reward and bias terms satisfy the following equation.

It is easy to verify by substitution that the values of g and v(i) in Equations (3) satisfy this equation.

Now apply a policy improvement step to verify that the policy is optimal. For i>M the policy improvement step looks for the action k which maximises

Since

and v(i+1)−v(i)=C if i⩾M, this expression is maximised when k is chosen so that i+k−d⩾M for all possible values of demand, d. Hence any k⩾2M−i is optimal.

For i⩽M the optimal policy improvement step looks for the action k that maximises

Since v(i+1)–v(i)>C if i<M, and v(i+1)−v(i)=C if i⩾M, this expression is maximised when k is chosen so that k⩾M. Hence, the policy given by Equation (5) is optimal.