Abstract
Flexible pricing plans are commonly observed in service industries. In this article, we argue that the presence of flexible pricing plans can be attributed to consumers being boundedly rational – these consumers do not always select the best available option; rather, they select better options more often. In our model, the seller faces consumers who are heterogeneous in their degrees of intertemporal inconsistency – their ultimate actions can be different from their intended actions. We show that, in response to these boundedly rational consumers the seller may be able to extract more profit by setting different prices in different periods and allowing the consumers to self-select which period to pay. Moreover, a single pricing plan may emerge as an optimal pricing scheme even when the consumers are heterogeneous in their degrees of rationality and the seller is not fully aware of the consumers’ types. We further show that the pricing patterns depend primarily on the relative discounting factor between the seller and the consumers.




Similar content being viewed by others
Notes
Flexible pricing is commonly adopted by conference organizers. As an another example, the 2009 INFORMS conference on O.R. practice has an early registration deadline, 10 April. Participants who register before the deadline pays $970 while participants who register after it pays $1070. Moreover, INFORMS members enjoy a $100 discount, that is they pay $870 to register before the deadline and $970 to register after it.
We thank an anonymous reviewer for this suggestion.
We now give an example to show that our model is suitable for competitors who order different pricing strategies as well as services that consumers value differently. Suppose there are three competitors (A, B and C) whose services are valued by consumers as μa, μb and μc respectively. Competitor A sells the service only in the first period at price pa1 while Competitor B sells the service only in the second period at price p2b. Competitor C, on the other hand, offers a pricing plan {p1c, p2c}. For a type-i consumer, her utility from accepting Competitor A's order is μa−p1a and that from Competitor B's order is μb−δ c p2b. The consumer's expected utility from accepting Competitor C's offer is (μc−p1c) × q1+(μc−δ c p2c) × q2, where
 and q2=1−q1. Thus, the best outside option (μi0) is type-dependent and in this example equals to the maximum of the three (expected) utilities.
and q2=1−q1. Thus, the best outside option (μi0) is type-dependent and in this example equals to the maximum of the three (expected) utilities.The derivation of the equation is shown below:

The derivation of the second-order derivative is as follows:

References
Anderson, S., Goeree, J. and Holt, C. (1998) Rent seeking with bounded rationality: An analysis of the all-pay auction. Journal of Political Economy 106 (4): 828–853.
Bansal, M. and Maglaras, C. (2009) Dynamic pricing when customers strategically time their purchase: Asymptotic optimality of a two-price policy. Journal of Revenue & Pricing Management 85 (1): 15–30.
Benabou, R. and Tirole, J. (2009, May) Over my dead body: Bargaining and the price of dignity. American Economic Review 99 (2): 459–465.
Burnetas, P., Gilbert, S. and Smith, C. (2007) Quantity discounts in single-period supply contracts with asymmetric demand information. IIE Transactions 39: 465–479.
Cachon, G. and Zhang, F. (2006) Procuring fast delivery: Sole-sourcing with information asymmetry. Management Science 52: 881–896.
Chaturvedi, A. and Martínez-de-Albéniz, V. (2009) Optimal procurement design in the presence of supply risk. Manufacturing & Service Operations Management, advance online publication 18 February 2011, doi: 10.1287/msom.1100.0319.
Chen, K. and Hogg, T. (2009) Modeling risky economic decision-making with bounded rationality. forthcoming in the Proceedings of AAAI Spring Symposium 2009 Human Behavior Modeling.
Corbett, C. and de Groote, X. (2000) A supplier's optimal quantity discount policy under asymmetric information. Management Science 46: 444–450.
DellaVigna, S. (2009) Psychology and economics: Evidence from the field. Journal of Economic Literature 47 (2): 315–372.
DellaVigna, S. and Malmendier, U. (2004) Contract design and self-control: Theory and evidence. The Quarterly Journal of Economics 119 (2): 353–402.
Deshpande, V., Schwarz, L., Atallah, M., Blanton, M. and Frikken, K. (2011) Outsourcing manufacturing: Secure price-masking mechanisms for purchasing component parts. Production and Operations Management 20 (2): 165–180.
Eliaz, K. and Spiegler, R. (2007) A mechanism-design approach to speculative trade. Econometrica 75 (3): 875–884.
Filiz-Ozbay, E. (2008) Incorporating Unawareness into Contract Theory. Working paper, University of Maryland.
Gul, F. and Pesendorfer, W. (2001, November) Temptation and self-control. Econometrica 69 (6): 1403–1435.
Ha, A. (2001) Supplier-buyer contracting: Asymmetric cost information and cutoff level policy for buyer participation. Naval Research Logistics 48: 41–64.
Han, S., Gupta, S. and Lehmann, D. (2001) Consumer price sensitivity and price thresholds. Journal of Retailing 77 (4): 435–456.
Heifetz, A., Meier, M. and Schipper, B. (2009) Dynamic Unawareness and Rationalizable Behavior. Working paper, The Open University of Israel.
Iyer, A., Schwarz, L. and Zenios, S. (2005) A principal-agent model for product specification and production. Management Science 51: 106–119.
Kostamis, D., Beil, D. and Duenyas, I. (2009) Total-cost procurement auctions: Impact of suppliers’ cost adjustments on auction format choice. Management Science 55 (12): 1985–1999.
Koszegi, B. and Rabin, M. (2006, November) A model of reference-dependent preferences. The Quarterly Journal of Economics 121 (4): 1133–1165.
Laffont, J. and Martimort, D. (2002) The Theory of Incentives: The Principal-Agent Model. Princeton, NJ: Princeton University Press.
Laffont, J. and Tirole, J. (1990) Adverse selection and renegotiation in procurement. The Review of Economic Studies 57 (4): 597–625.
Lim, N. and Ho, T. (2007) Designing price contracts for boundedly rational customers: Does the number of blocks matter? Marketing Science 26 (3): 312–326.
McKelvey, R. and Palfrey, T. (1995) Quantal response equilibria for normal form games. Games and Economic Behavior 10 (1): 6–38.
O'Donoghue, T. and Rabin, M. (1999) Incentives for procrastinators. Quarterly Journal of Economics 114: 769–816.
O'Donoghue, T. and Rabin, M. (2008) Procrastination on long-term projects. Journal of Economic Behavior and Organization 66: 161–175.
Orhun, A. (2009) Optimal product line design when consumers exhibit choice set-dependent preferences. Marketing Science 28 (5): 868–886.
Ozbay, E.Y. (2006) Unawareness and strategic announcements in games with uncertainty. International Journal of Game Theory 4: 1029–1050.
Ozdenoren, E., Salant, S. and Silverman, D. (2006) Willpower and the Optimal Control of Visceral Urges. NBER Working Paper.
Rabin, M. (1998) Psychology and economics. Journal of Economic Literature 36 (1): 11–46.
Rubinstein, A. (1993) On price recognition and computational complexity in a monopolistic model. Journal of Political Economy 101 (3): 473–484.
Su, X. (2008) Bounded rationality in newsvendor models. Manufacturing & Service Operations Management 10 (4): 566–589.
Taylor, T. and Xiao, W. (2010) Does a manufacturer benefit from selling to a better-forecasting retailer? Management Science 56 (9): 1584–1598.
Tirole, J. (2009) Cognition and incomplete contracts. American Economic Review 99 (1): 265–294.
von Thadden, E. and Zhao, X. (2009) Incentives for Unaware Agents. Technical report, University of Mannheim (mimeo).
Wan, Z. and Beil, D. (2009) RFQ auctions with supplier qualification screening. Operations Research 57 (4): 934–949.
Yang, Z., Aydin, G., Babich, V. and Beil, D. (2009) Supply disruptions, asymmetric information, and a backup production option. Management Science 55 (2): 192–209.
Zhang, H. and Zenios, S. (2008) A dynamic principal-agent model with hidden information: Sequential optimality through truthful state revelation. Operations Research 56 (3): 681–696.
Zhou, S.X., Tao, Z., Zhang, N.B. and Cai, G. (2009) Reverse Auction Procurement with Flexible Noncompetitive Contracts. Working paper, Chinese University of Hong Kong.
Acknowledgements
We thank Ian Yeoman (the editor) and the review team for their detailed comments and many valuable suggestions that have significantly improved the quality of the article. We also benefited from the discussions with Qian Liu, George Shanthikumar, Zuo-Jun Max Shen, Xuanming Su and Xiaojian Zhao. All remaining errors are our own.
Author information
Authors and Affiliations
Additional information
2joined the IEOR Department at UC Berkeley after completing his PhD in Operations Management from New York University. He also holds master's and bachelor's degrees of Electrical Engineering from National Taiwan University. He is a recipient of NYU teaching excellence award, Second place of INFORMS JFIG paper competition, the Harold MacDowell Award from Stern School, Meritorious Service Awards from Management Science and MSOM. His current research interests lie in operations-marketing interface, auctions, supply chain management and competitive strategies.
APPENDIX
APPENDIX
Proofs of Propositions 1, 2 and 3
Recall that the participation constraint can be written as

which, after replacing ui2 by v
i
+ui1, can be simplified as follows:  . The seller's problem is therefore to find a pricing plan that solves the following problem:
. The seller's problem is therefore to find a pricing plan that solves the following problem:

Since ui2=v i +ui1 and δ s pi2=δ(pi1−v i ), for a fixed value of v i , ui2 decreases as ui1 decreases and pi2 increases in pi1. Suppose that the participation constraint does not bind, the seller can decrease ui1 while keeping v i unchanged. ui2 decreases as a result. Since pi1=μ−ui1 and pi2=(μ−ui2)/δ c , both pi1 and pi2 increase and so does the seller's expected profit. Thus (PC-i) binds:

We can therefore represent utilities and prices in terms of v i :

Substituting these terms in the seller's objective, the seller's optimization problem becomes an unconstrained one:

where the third equation follows from  . The first-order condition on v
i
leads to
. The first-order condition on v
i
leads to

Let  and observe that D(0)=0 and D(v
i
) is negative for all other values of v
i
. Therefore,
and observe that D(0)=0 and D(v
i
) is negative for all other values of v
i
. Therefore,  and thus:
and thus:
-
When δ=1, (A.2) is satisfied for any v i , thus the seller's expected profit is μ−c regardless of the first and second period prices.
-
When δ<1 and γ i >1/μ, first order derivative with respect to v i is positive for all values of v i . Thus the optimal value of v i is −∞, the optimal pricing plan is {pi1F, pi2F}={μ,∞}, and the associated seller's expected profit is μ−c.
-
When δ>1 and γ i >1/μ, first order derivative with respect to v i is negative for all values of v i . Thus the optimal value of v i is ∞, the optimal pricing plan is {pi1F, pi2F}={∞, δμ}, and the associated seller's expected profit is δμ−c.
Notice that D(v i ) is symmetric with respect to the origin:

Its derivative,

is negative for positive values of v i and positive for negative values of v i . Thus, for all γ i <1/μ, there are exactly two solutions to (A.2). Let v i P>0 be the positive solution and v i N=−v i P be the negative solution to (A.2). Now we examine the second-order conditions on v i :


We see that (A.3) is negative when δ<1 and positive when δ>1 while (A.4) is negative when δ>1 and positive when δ<1. Thus v i P is a local maximizer when δ<1 while v i N is a local maximizer when δ>1. We now show that Π i F monotonically decreases in γ i :

Thus, there exists a cutoff type, γ lp , such that the corresponding v lp (>0) satisfy Π i F(v lp )=μ−c. When δ<1, v i P is the global maximizer for all γ i <γ lp . we now look for the condition for γ lp and v lp :

Thus, γ lp and v lp satisfy the following equations simultaneously:

Similarly, there exists a cutoff type, γ mp , such that the corresponding v mp (<0) satisfy Π i F(v mp )=δμ−c. When δ>1, γ mp is the global maximizer for all γ i <γ mp ,

Thus, γ mp and v mp satisfy the following equations simultaneously:

Proof of Proposition 5
First, we re-write the optimization problem as

Notice that when δ<1, the {pi1, pi2}={μ,∞}, ∀i=1,2, is a feasible solution to (A.7). The seller's expected profit associated with this candidate solution is μ−c. We thus focus on searching for a solution that yields an expected profit that is higher than μ−c. Similarly, {pi1, pi2}={∞, δμ}, ∀i=1,2, is a feasible solution to (A.7) when δ>1. The seller's expected profit associated with this candidate solution is δμ−c, and we search for a solution that yields a higher than δμ−c expected profit. We now show that both (PC-2) and (IC-1,2) bind at optimality by contradiction. Suppose (PC-2):  does not bind. In this case, the seller can increase his expected profit by decreasing u21 and u22 while keeping v2 unchanged (v2=u22−u21). This will increase the objective value without violating any constraint. Thus (PC-2) binds, that is
does not bind. In this case, the seller can increase his expected profit by decreasing u21 and u22 while keeping v2 unchanged (v2=u22−u21). This will increase the objective value without violating any constraint. Thus (PC-2) binds, that is 
Given this, we can write type-2 consumers’ utilities and payments in terms of a single variable v2:

We then consider (IC-1,2):

This constraint must bind at optimality as well; otherwise, the seller can increase his expected profit by decreasing u11 and u12 while keeping v2 unchanged. When v2>0,  and thus
and thus  When v2<0,
When v2<0,  and thus
and thus  (IC-1,2) can then be written as the following equality constraint:
(IC-1,2) can then be written as the following equality constraint:

In the remaining proof, we divide our analysis into two cases: (1) v2 is positive and (2) v2 is negative. There are two subcases in each case: max{u11, u12}=u11 and max{u11, u12}=u12 in each case. We now look at each of them separately:
Case 1: v2 is positive.
Subcase 1.1:  . In this case,
. In this case,  A fully rational consumer purchases in the period when the price is lower, and thus the first-period price has to be non-negative in the optimal solution; otherwise, the seller can set the second-period price to be negative instead
A fully rational consumer purchases in the period when the price is lower, and thus the first-period price has to be non-negative in the optimal solution; otherwise, the seller can set the second-period price to be negative instead  to obtain a smaller loss. Thus, p11⩾0, that is
to obtain a smaller loss. Thus, p11⩾0, that is  Notice that if we set v1=v2, we obtain u11=u12−v1=u12−v2=u22−v2=u21. In this case,
Notice that if we set v1=v2, we obtain u11=u12−v1=u12−v2=u22−v2=u21. In this case,

that is, (IC-2,1) is satisfied. The seller's expected profit function can be written as an unconstrained optimization function with a single variable (v2):

First, let us compare the seller's expected profit with μ−c – obtained from a candidate solution {pi1, pi2}={μ,∞}, ∀i=1,2, when δ<1:

where the inequality follows from the fact that p11⩾0 and δ<1. Since  , setting the first-period price to
, setting the first-period price to  is never optimal when δ<1. Next, we compare the seller's expected profit with δμ−c – obtained from a candidate solution {pi1, pi2}={∞, δμ} when δ>1:Footnote 4
is never optimal when δ<1. Next, we compare the seller's expected profit with δμ−c – obtained from a candidate solution {pi1, pi2}={∞, δμ} when δ>1:Footnote 4

Thus, it is optimal to set v2 to infinity when the first-period price to 
Subcase 1.2:  In this case,
In this case,  Moreover, (PC-1):
Moreover, (PC-1):

is satisfied as well. Substituting all the utilities and payments by the aforementioned functions of v2, the seller's expected profit function can be written as:

Observe that when δ>1,

Since ΠS−(δμ−c)<0, it is optimal to set v2 to ∞. When δ<1, (A.8) is greater than equation (A.9) and  in which case setting the second-period price to
in which case setting the second-period price to  is never optimal. When δ<1 and
is never optimal. When δ<1 and  the first-order condition on v2 yields
the first-order condition on v2 yields

We can rewrite (A.10) as follows:

Let v2P be the positive solution of (A.11), the second-order condition is as followsFootnote 5:

The equation above is only negative when ρ1 is sufficiently small, that is if

we obtain that

The equation above shows that ΠS monotonically decreases in γ i .
Case 2: v2 is negative.
Subcase 2.1:  With the same reasoning as Subcase 1.1,
With the same reasoning as Subcase 1.1,  The seller's expected profit function can be written as
The seller's expected profit function can be written as

Let us first compare the seller's expected profit with μ−c – obtained from a candidate solution {pi1, pi2}={μ,∞}∀ i=1,2 when δ<1:

Therefore, setting the second-period price v2 to −∞ is optimal. We now compare the seller's expected profit with δμ−c, which is obtained from the candidate solution {pi1, pi2}={∞, δμ}, ∀ i=1, 2 when δ>1:

Thus, setting first-period price to  is never optimal.
is never optimal.
Subcase 2.2:  In this case,
In this case,  The seller's optimization problem can be written as
The seller's optimization problem can be written as

Observe that when δ<1,

Thus, setting the second-period price v2 to −∞ is optimal. When δ>1, The expression of ΠS in (A.12) is greater than that in (A.13) and  Therefore, setting the second-period price to
Therefore, setting the second-period price to  is never optimal. When δ>1 and
is never optimal. When δ>1 and  the first-order condition on v2 yields:
the first-order condition on v2 yields:

We can re-write (A.14) as

Let v2N be the negative solution of equation (A.15), the second-order condition is as follows:

Equation (A.16) is negative when ρ1 is sufficiently small. Specifically,

We now show that ΠS monotonically decreases in γ i :

Finally, we can pin down the cutoff thresholds ρ1c and vc. They are the solutions that solve (A.17) and (A.18) for δ<1:


and for δ>1:

Proof of Proposition 6
Since ui2=ui1+v i , (PC-i) and (IC-i, j) can be simplified as follows:


Now we show that (PC-2) and (IC-1,2) imply (PC-1):

Recall that both (PC-2) and (IC-1,2) bind, otherwise the seller can raise prices to decrease consumers’ utilities until they bind while increasing his expected profit. Define  a positive function for all values of v. From the binding (PC-2) and (IC-1,2), we obtain that
a positive function for all values of v. From the binding (PC-2) and (IC-1,2), we obtain that


Recall that the objective function is

After substituting the prices and utilities by functions of {v i }'s, we can express the reduced program of the seller's optimization problem as follows:


ΠS can then be written as follows:

Let

represent the maximum expected profit extracted from type-1 consumer when the seller is able to identify the consumer's type. Recall that γ c is the cutoff value of γ above which the seller's expected profit is bounded above by μ−c. Thus, R1*⩽μ−c for all γ1⩾γ c . Since F(v2)⩾0 for all values of v2,

Similarly, let

represent the maximum revenue extracted from type-2 consumer when the consumer's type is known. Since γ2<γ c , R2*>μ. From the above discussions, we obtain an upper bound of the excess expected profit the seller can obtain from offering a menu of contracts:

Notice that when ρ1=1, only type-1 consumers are present in the market. ΠS becomes ΠF and thus ΠS=μ−c. When ρ1=0, ΠS=R2*>μ−c.
Let  and
and  be the cutoff value such that
be the cutoff value such that  For any value of
For any value of  Thus, it is optimal for the seller to simply offer a single pricing plan {pi1, pi2}={μ, ∞}. □
Thus, it is optimal for the seller to simply offer a single pricing plan {pi1, pi2}={μ, ∞}. □
Proof of Proposition 7
The participation constraint can be simplified as 
This constraint must bind, thus we can re-write utilities and prices in terms of v i :


Substituting these terms in the seller's objective, the seller's optimization problem becomes an unconstrained one:

The first-order condition on v i leads to

Notice that the above equation is the same as equation (A.2) in the basic case if we replace μ−μi0 by μ. Thus, we can directly borrow results from the proofs of Propositions 1, 2 and 3:
-
When δ=1, equation (A.19) is satisfied for any v i , thus the seller's expected profit is μ−μi0−c regardless of the first and second period prices.
-
When δ<1 and γ i >1/μ−μi0, first-order derivative with respect to v i is positive for all values of v i . Thus the optimal value of v i is −∞, the optimal pricing plan is (pi1C, pi2C)=(μ−μi0,∞), and the associated seller's expected profit is μ−μi0−c.
-
When δ>1 and γ i >1/μ, first-order derivative with respect to v i is negative for all values of v i . Thus the optimal value of v i is ∞, the optimal pricing plan is (pi1F, pi2F)=(∞,δ(μ−μi0)), and the associated seller's expected profit is δ(μ−μi0)−c.
Let v i CP>0 be the positive solution to equation (A.19) and v i CN=−v i CP be the negative solution. Use the same mathematical deduction as that in the proofs of Propositions 1, 2 and 3, v i CP is a local maximizer when δ<1 while v i CN is a local maximizer when δ>1. Thus, there exists a cutoff type γ lp C such that its corresponding ν lp C satisfy Π i C(v lp C)=μ−μi0−c and that v i CP is the global maximizer for all γ i <γ lp C. The cutoff values, γ lp C and v lp C, satisfy the following equations simultaneously:

It is worth noting that if we replace the term (μ−μi0) with μ, equation (A.20) is the same as equation (A.5). This means that when the best outside option gives type-i consumer a utility of μi0, the pricing plan is the same as the case of no competition and the consumer's valuation is μ−μi0. Combining the two equations above, we obtain a relationship between γ lp C and v lp C:

The equation above shows that γ ip Cv ip C is constant regardless the value of μ−μi0, thus v lp C decreases in μi0 while γ lp C increases in μi0.
Similarly, there exists a cutoff type γ mp C such that the corresponding v mp C satisfy Π i C(v mp C)=δ(μ−μi0)−c and that γ mp C is the global maximizer for all γ i <γ mp C. The cutoff values, γ mp C and v mp C, satisfy the following equations simultaneously:

With the same reasoning as above, we can conclude that the absolute value of v mp C decreases in μi0 while γ mp C increases in μi0. Combine both cases we can conclude that the price dispersion decreases in μi0 while the cutoff valuations increase in μi0 increases. □
Proof of Proposition 8
Before we solve the optimization problem, let us first compare the consumers’ expected utility for a given pricing plan {p1, p2}. The expected utility for a low-valuation consumer is

where v=p1−δ c p2. The expected utility for a high-valuation consumer is

Let μ d =μ1−μ2, the above equation can be written as

Owing to the common degree of rationality, the probability of a consumer chooses to purchase in period 1 depends only on the adjusted price difference. A high-valuation consumer behaves the same as the low-valuation consumer does provided that the pricing plan induce both types of consumer to participate. Moreover, the expected utility of a high valuation consumer is higher than that of a low-valuation consumer by a fixed amount (μ d ) for a given pricing plan. With that insight in mind, we can move on to solve the problem. Let v i =ui2−ui1=pi1−δ c pi2. Since μ1−p21=(μ1−μ2)+(μ2−p21)=μ d +u21 and μ1−δ c p22=(μ1−μ2)+(μ2−δ c p22)=μ d +u22, (IC-1,2) can thus be simplified as

and similarly (IC-2,1) can be written as

It is clear that (PC-2) binds, and thus  We can write p21 in terms of μ2 and v2:
We can write p21 in terms of μ2 and v2:  Similarly, δ
c
p22 can be written as
Similarly, δ
c
p22 can be written as  Suppose (IC-1,2) binds, then
Suppose (IC-1,2) binds, then  , that is,
, that is,  Consequently, p11 equals
Consequently, p11 equals  and δ
c
p12 equals
and δ
c
p12 equals 
It is easy to verify that both (PC-1) and (IC-2,1) are satisfied:

The expected profit function can then be written as

The derivatives with respect to v1 and v2 are as follows:


Let v1p>0 and v1n<0 be the two solutions for (A.25) and v2p>0 and v2n<0 for (A.26). Since (A.25) and (A.26) must be satisfied simultaneously, v1p=v2p=vp and v1n=v2n=vn. For the expected profit function to achieve its maximum, we also need

Thus, the local maximizers are (v1, v2)=(vp, vp) when δ<1 and (v1, v2)=(vn, vn) when δ>1.
Case 1: δ<1

A candidate solution is the corner solution (v1, v2)=(−∞,−∞), with a profit of μ2−c. ΠH(vp, vp) is a global maximum if it is greater than μ2−c. We need to compare to the case where the seller only serve type-1 consumers. Here only (PC-1) needs to be satisfied; thus,  Let Π1 be the seller's expected profit, which can be written as
Let Π1 be the seller's expected profit, which can be written as

where v1 satisfies  Since Π1(v1) decreases in ρ1, there exists a cutoff value for ρ1 such that Π1(v1)=ΠH(vp, vp),
Since Π1(v1) decreases in ρ1, there exists a cutoff value for ρ1 such that Π1(v1)=ΠH(vp, vp),

To summarize, the seller is interested in serving high-valuation consumers when the proportion is large enough (ρ1>ρ1c), and when the proportion of high-valuation consumers is low, the seller sets the price as if it only serves type 2 consumers.
Case 2: δ>1
In this case, we obtain

The corner solution (v1, v2)=(∞,∞) gives rise to the expected payoff ΠH(∞,∞)=δμ2−c. Thus, ΠH(vn, vn) is a global maximum if it is greater than δμ2−c. □
Rights and permissions
About this article
Cite this article
Cai, W., Chen, YJ. Intertemporal pricing with boundedly rational consumers. J Revenue Pricing Manag 11, 421–452 (2012). https://doi.org/10.1057/rpm.2011.14
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1057/rpm.2011.14


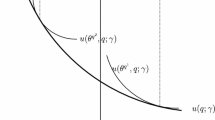


 and q2=1−q1. Thus, the best outside option (μi0) is type-dependent and in this example equals to the maximum of the three (expected) utilities.
and q2=1−q1. Thus, the best outside option (μi0) is type-dependent and in this example equals to the maximum of the three (expected) utilities.
